
如图10-1,在平面直角坐标系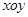 中,点
中,点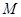 在
在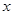 轴的正半轴上, ⊙
轴的正半轴上, ⊙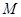 交
交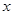 轴于
轴于 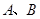 两点,交
两点,交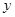 轴于
轴于 两点,且
两点,且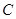 为
为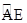 的中点,
的中点,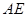 交
交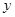 轴于
轴于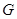 点,若点
点,若点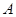 的坐标为(-2,0),
的坐标为(-2,0),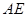
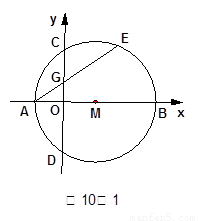
(1)(3分)求点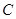 的坐标.
的坐标.
(2)(3分)连结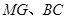 ,求证:
,求证: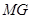 ∥
∥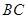
(3)(4分) 如图10-2,过点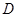 作⊙
作⊙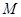 的切线,交
的切线,交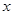 轴于点
轴于点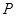 .动点
.动点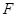 在⊙
在⊙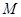 的圆周上运动时,
的圆周上运动时,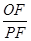 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
(1)(0,4)
(2)证明略
(3)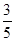
【解析】解(1)方法(一)∵直径AB⊥CD
∴CO=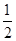 CD
……1分
CD
……1分
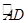 =
=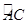
∵C为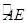 的中点
的中点
∴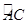 =
=
∴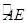 =
=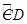
∴CD=AE ……2分
∴CO=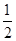 CD=4
CD=4
∴C点的坐标为(0,4) ……3分
方法(二)连接CM,交AE于点N
∵C为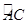 的中点,M为圆心
的中点,M为圆心
∴AN=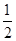 AE=4
……1分
AE=4
……1分
CM⊥AE
∴∠ANM=∠COM=90°
在△ANM和△COM中:
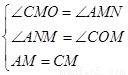
∴△ANM≌△COM ……2分
∴CO=AN=4
∴C点的坐标为(0,4) ……3分
解(2)设半径AM=CM=r,则OM=r-2
由OC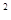 +OM
+OM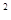 =MC
=MC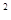 得:
得:
4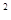 +(r-2)
+(r-2)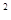 =r
=r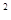
解得:r=5 ……1分
∵∠AOC=∠ANM=90°
∠EAM=∠MAE
∴△AOG∽△ANM
∴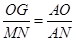
∵MN=OM=3
即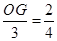
∴OG=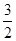 ……2分
……2分
∵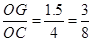
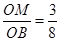
∴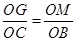
∵∠BOC=∠BOC
∴△GOM∽△COB
∴∠GMO=∠CBO
∴MG∥BC ……3分
(说明:直接用平行线分线段成比例定理的逆定理不扣分)
解(3)连结DM,则DM⊥PD,DO⊥PM
∴△MOD∽△MDP,△MOD∽△DOP
∴DM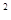 =MO·MP;
=MO·MP;
DO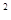 =OM·OP(说明:直接使用射影定理不扣分)
=OM·OP(说明:直接使用射影定理不扣分)
即4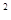 =3·OP
=3·OP
∴OP=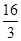 ……1分
……1分
当点F与点A重合时: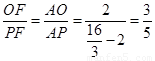
当点F与点B重合时: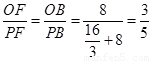 ……2分
……2分
当点F不与点A、B重合时:连接OF、PF、MF
∵DM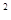 =MO·MP
=MO·MP
∴FM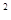 =MO·MP
=MO·MP
∴
∵∠AMF=∠FMA
∴△MFO∽△MPF
∴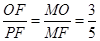
∴综上所述,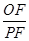 的比值不变,比值为
的比值不变,比值为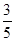 ……4分
……4分


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
如图10-1,在平面直角坐标系![]() 中,点
中,点![]() 在
在![]() 轴的正半轴上,⊙
轴的正半轴上,⊙![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于
轴于![]() 两点,且
两点,且![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 轴于
轴于![]() 点,若点
点,若点![]() 的坐标为(-2,0),
的坐标为(-2,0),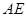
![]()
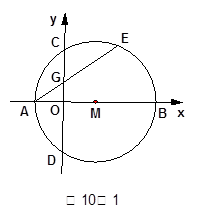
(1)(3分)求点![]() 的坐标.
的坐标.
(2)(3分)连结![]() ,求证:
,求证:![]() ∥
∥![]()
(3)(4分) 如图10-2,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 轴于点
轴于点![]() .动点
.动点![]() 在⊙
在⊙![]() 的圆周上运动时,
的圆周上运动时,![]() 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
查看答案和解析>>
科目:初中数学 来源: 题型:
如图10-1,在平面直角坐标系中,点
在
轴的正半轴上, ⊙
交
轴于
两点,交
轴于
两点,且
为
的中点,
交
轴于
点,若点
的坐标为(-2,0),
(1)(3分)求点的坐标.
(2)(3分)连结,求证:
∥
(3)(4分) 如图10-2,过点作⊙
的切线,交
轴于点
.动点
在⊙
的圆周上运动时,
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
查看答案和解析>>
科目:初中数学 来源:2006年高级中等学校招生全国统一考试数学卷(广东深圳) 题型:解答题
如图10-1,在平面直角坐标系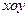 中,点
中,点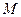 在
在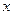 轴的正半轴上, ⊙
轴的正半轴上, ⊙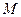 交
交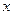 轴于
轴于 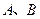 两点,交
两点,交 轴于
轴于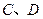 两点,且
两点,且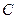 为
为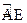 的中点,
的中点,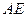 交
交 轴于
轴于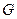 点,若点
点,若点 的坐标为(-2,0),
的坐标为(-2,0),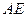


(1)(3分)求点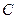 的坐标.
的坐标.
(2)(3分)连结 ,求证:
,求证: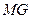 ∥
∥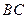
(3)(4分) 如图10-2,过点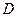 作⊙
作⊙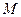 的切线,交
的切线,交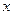 轴于点
轴于点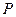 .动点
.动点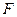 在⊙
在⊙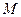 的圆周上运动时,
的圆周上运动时,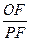 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
查看答案和解析>>
科目:初中数学 来源:2011年浙江省衢州市共同体初一第一学期期末数学卷 题型:解答题
如图10-1,在平面直角坐标系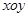 中,点
中,点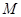 在
在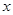 轴的正半轴上,
⊙
轴的正半轴上,
⊙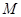 交
交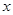 轴于
轴于
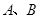 两点,交
两点,交 轴于
轴于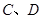 两点,且
两点,且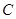 为
为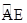 的中点,
的中点, 交
交 轴于
轴于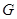 点,若点
点,若点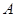 的坐标为(-2,0),
的坐标为(-2,0),
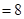
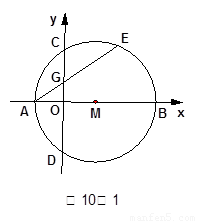
(1)(3分)求点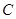 的坐标.
的坐标.
(2)(3分)连结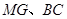 ,求证:
,求证: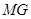 ∥
∥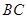
(3)(4分) 如图10-2,过点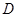 作⊙
作⊙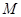 的切线,交
的切线,交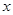 轴于点
轴于点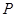 .动点
.动点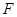 在⊙
在⊙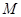 的圆周上运动时,
的圆周上运动时,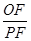 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com