
将 绕点
绕点 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为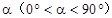 ,旋转后使各边长变为原来的
,旋转后使各边长变为原来的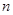 倍,得到
倍,得到 ,我们将这种变换记为[
,我们将这种变换记为[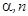 ].
].
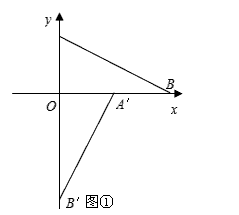
(1)如图①,对 作变换[
作变换[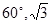 ]得
]得 ,则
,则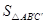 :
: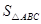 = ___;直线
= ___;直线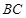 与直线
与直线 所夹的锐角为 __ °;
所夹的锐角为 __ °;

图①
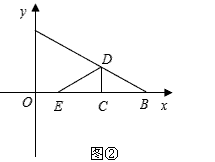
(2)如图②, 中,
中,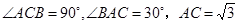 ,对
,对 作变换[
作变换[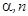 ]得
]得 ,使得四边形
,使得四边形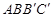 为梯形,其中
为梯形,其中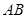 ∥
∥ ,且梯形
,且梯形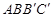 的面积为
的面积为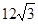 ,求
,求 和
和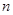 的值.
的值.

图②
(1)3,60;(2)60°,4.
【解析】
试题分析:根据题意知△ABC∽△AB′C′,因此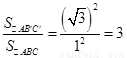 ;直线BC与B′C′所夹的锐角的度数为:360°-90°-90°-60°-120°=60°.
;直线BC与B′C′所夹的锐角的度数为:360°-90°-90°-60°-120°=60°.
(2)因为AB∥B′C′,∠C′=90°,∠BAC=30°,所以∠CAC′=60°;由△ABC∽△AB′C′及梯形面积可求出n的值.
试题解析:(1) 3 , 60
(2) 由题意可知:△ABC∽△AB′C′,
∴∠C′=∠C=90°,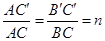
∵AB∥B′C′,
∴∠BAC′=90°
∴
在Rt△ABC中,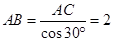 ,
,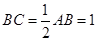
∴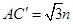 ,
,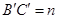
∴在直角梯形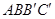 K中,
K中,
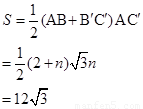
∴n=4,n=-6(舍去)
∴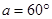 ,n=4
,n=4
考点:1.旋转;2相似三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 (2012•栖霞区一模)如图,已知在△OBC中,∠BOC=90°,且OB=OC,△OAB是正三角形,将△OAB绕点O按逆时针方向旋转得到△OCD,旋转角为a(0°<a<180°),则∠a=
(2012•栖霞区一模)如图,已知在△OBC中,∠BOC=90°,且OB=OC,△OAB是正三角形,将△OAB绕点O按逆时针方向旋转得到△OCD,旋转角为a(0°<a<180°),则∠a=查看答案和解析>>
科目:初中数学 来源:辽宁省中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年河北省石家庄市九年级第二次模拟考试数学试卷(解析版) 题型:填空题
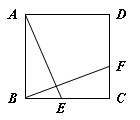
如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向转到△BCF,旋转角为a(0°<a<180°),则∠a=______.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省海安县五校九年级第一学期期中考试数学卷 题型:填空题
如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向转到△BCF,旋转角为a(0°<a<180°),则∠a= ▲

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com