

分析 (1)分别以点A、O为圆心,AO长为半径画弧,两弧交于点C,作射线OC即可;
(2)分OC在∠AOB内部和外部两种情况,由角平分线的定义可得∠COD=$\frac{1}{2}$∠BOC、∠COE=$\frac{1}{2}$∠AOC,分别依据∠DOE=∠COD+∠COE、∠DOE=∠COD-∠COE可得答案;
(3)与(2)同理可得.
解答 解:(1)如图所示,∠AOC或∠AOC′即为所求,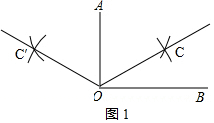
当OC在∠AOB内部时,∠BOC=∠AOB-∠AOC=30°,
当OC在∠AOB外部时,∠BOC=∠AOB+∠AOC=150°,
故答案为:30°或150°;
(2)当OC在∠AOB内部时,如图2,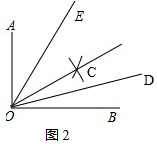
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=$\frac{1}{2}$∠BOC=15°,∠COE=$\frac{1}{2}$∠AOC=30°,
∴∠DOE=∠COD+∠COE=45°;
当OC在∠AOB外部时,如图3,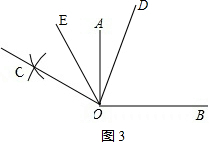
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=$\frac{1}{2}$∠BOC=75°,∠COE=$\frac{1}{2}$∠AOC=30°,
∴∠DOE=∠COD-∠COE=45°;
故答案为:45°;
(3)如图2,当OC在∠AOB内部时,
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠COD+∠COE
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(90°-2α)+$\frac{1}{2}$•2α
=45°;
如图3,当OC在∠AOB外部时,
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠COD-∠COE
=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(90°+2α)-$\frac{1}{2}$•2α
=45°.
点评 本题主要考查角平分线的定义,熟练掌握角平分线的定义及角的运算是解题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若$\frac{a}{2}$=$\frac{b}{4}$,则a=2b | D. | 若a2=b2,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
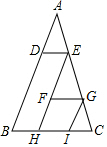 如图,在△ABC中,DE∥FG∥BC,GI∥EF∥AB,若△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,则△ABC的面积为162cm2.
如图,在△ABC中,DE∥FG∥BC,GI∥EF∥AB,若△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,则△ABC的面积为162cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
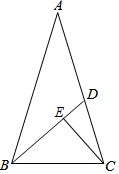 如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )
如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}+3}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知BD是⊙O的直径,点A、C均在⊙O上,连接AO、DC,若$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则圆周角∠BDC的大小是( )
如图,已知BD是⊙O的直径,点A、C均在⊙O上,连接AO、DC,若$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则圆周角∠BDC的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com