[题目]如图.△ABC中.∠A=30°.∠B=62°.CE平分∠ACB.CD⊥AB于D.DF⊥CE于F.求∠CDF的度数．题目和参考答案——青夏教育精英家教网—

【题目】如图，△ABC中，∠A=30°，∠B=62°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，求∠CDF的度数．

【答案】74°．

【解析】试题分析：首先根据三角形的内角和定理求得∠ACB的度数，以及∠BCD的度数，根据角的平分线的定义求得∠BCE的度数，则∠ECD可以求解，然后在△CDF中，利用内角和定理即可求得∠CDF的度数．

试题解析：解：∵∠A=40°，∠B=72°，∴∠ACB=180°﹣（∠A+∠B）=180°﹣（30°+62°）=180°﹣92°=88°，∵CE平分∠ACB，∴∠ECB=∠ACB=44°，∵CD⊥AB于D，∴∠CDB=90°，∴∠BCD=90°﹣∠B=90°﹣62°=28°，∴∠ECD=∠ECB﹣∠BCD=44°﹣28°=16°，∵DF⊥CE于F，∴∠CFD=90°，∴∠CDF=90°﹣∠ECD=90°﹣16°=74°．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】2018年秋，珊瑚中学开启“珊中大阅读”活动,为了充实漂流书吧藏书,号召全校学生捐书,得到各班的大力支持.同时,本部校区的两个年级组也购买藏书充实学校图书室,初二年级组购买了甲、乙两种自然科学书籍若干本,用去8315元;初一年级买了A、B两种文学书籍若干本,用去6138元。其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲种书的单价比乙种书的单价多7元,则甲种书籍比乙种书籍多买了_____________本.

查看答案和解析>>

科目：初中数学 来源： 题型：

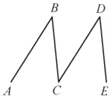
【题目】如图，如果AB∥CD，∠B＝37°，∠D＝37°，那么BC与DE平行吗？完成下面解答过中的填空或填写理由．

解：∵AB∥CD （已知），

∴∠B＝　　（　　）

∵∠B＝∠D＝37°（已知）

∴　　＝∠D （等量代换）

∴BC∥DE （　　）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】图1为北京城市女生从出生到15岁的平均身高统计图，图2是北京城市某女生从出生到12岁的身高统计图．
请你根据以上信息预测该女生15岁时的身高约为，你的预测理由是．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】三角板是学习数学的重要工具，将一副三角板中的两块直角三角板的直角顶点按如图方式叠放在一起，当且点在直线的上方时，解决下列问题：（友情提示：，，．

（1）①若，则的度数为　　；

②若，则的度数为　　；

（2）由（1）猜想与的数量关系，并说明理由．

（3）这两块三角板是否存在一组边互相平行？若存在，请直接写出的角度所有可能的值（不必说明理由）；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C，连接BC，∠P=∠B．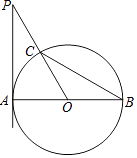
（1）求∠P的度数；
（2）连接PB，若⊙O的半径为a，写出求△PBC面积的思路．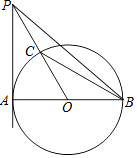

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知直线AB∥DF，∠D+∠B=180°，

（1）求证：DE∥BC；

（2）如果∠AMD=75°，求∠AGC的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知一次函数 y＝（m﹣2）x+3﹣m 的图象不经过第三象限，且 m 为正整数．

(1)求 m 的值．

(2)在给出的平面直角坐标系中画出该一次函数的图象．

(3)当﹣4＜y＜0 时，根据函数图象，求 x 的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】将一副三角板按如图摆放，其中△ABC为含有45度角的三角板，直线AD是等腰直角三角形ABC的对称轴，且将△ABC分成两个等腰直角三角形，DM、DN分别与边AB、AC交于E、F两点，有下列四个结论：①BD＝AD＝CD②△AED≌△CFD③BE+CF＝EF④S四边形AEDF＝AB2．其中正确结论是_____（填写正确序号）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学