
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
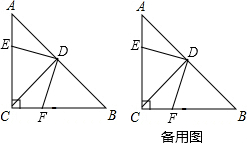 在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.
在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.
在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB=BC,要使△ABD≌△CBD,需要添加下列选项中的( )
如图,已知AB=BC,要使△ABD≌△CBD,需要添加下列选项中的( )| A. | ∠ABD=∠CBD | B. | ∠ADB=∠CDB | C. | ∠A=∠C | D. | BD=BD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )| A. | 0.1 | B. | 0.17 | C. | 0.33 | D. | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com