
【题目】等腰直角![]() 和等腰直角
和等腰直角![]() 分别在直线
分别在直线![]() 上.
上.
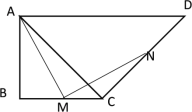
(1)如图所示,![]() 分别在线段
分别在线段![]() 上,若
上,若![]() ,求证:
,求证:![]() .
.
(2)若![]() 分别在线段
分别在线段![]() 外(还在直线
外(还在直线![]() 上),根据题意,画出图形,那么(1)的结论是否依然成立,若成立,写出证明过程;若不成立,说明原因;
上),根据题意,画出图形,那么(1)的结论是否依然成立,若成立,写出证明过程;若不成立,说明原因;
(3)如图,若![]() ,求证:
,求证:![]() .
.

【答案】(1)详见解析;(2)成立,详见解析;(3)详见解析
【解析】
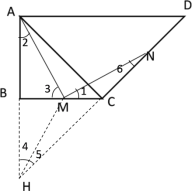
(1)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,先证出△BHC为等腰直角三角形,然后证出BC是
,先证出△BHC为等腰直角三角形,然后证出BC是![]() 的垂直平分线,根据垂直平分线的性质可得
的垂直平分线,根据垂直平分线的性质可得![]() ,然后根据等边对等角和等角对等边证出HM=MN,即可证出结论;
,然后根据等边对等角和等角对等边证出HM=MN,即可证出结论;
(2)根据题意,分点M在CB的延长线和点M在BC的延长线两种情况讨论,分别画出对应的图形,根据垂直平分线的性质、等边对等角和等角对等边分别证明即可;
(3)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,由(1)可得
,由(1)可得![]() 是
是![]() 的垂直平分线,然后根据等边对等角和等量代换即可证出
的垂直平分线,然后根据等边对等角和等量代换即可证出![]() ,从而证出结论.
,从而证出结论.
解:(1)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]()
∵等腰直角![]() 和等腰直角
和等腰直角![]()
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() ,
,
![]() ,
,
而![]() ,
,
![]()
![]() ,
,
![]()
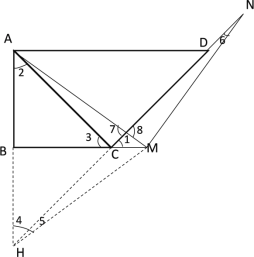
(2)成立,证明如下
第一种情况:如图所示
延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ;
;
由(1)可得:![]() ,
,![]() ,
,
![]() ,
,
显然![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,且
,且![]() ;
;
![]() ,
,
![]() ,
,
![]()

第二种情况:
易证显然![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,
,
即![]() ,
,
![]()
而![]() ,∠7=∠8,
,∠7=∠8,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
(3)延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
由(1)可得![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
∴![]()
而![]() ,
,
![]() ,
,
又![]() ,
,
![]()
而![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.



 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
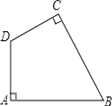
【题目】如图,在四边形ABCD中,∠A=∠C=90°.
(1)用直尺和圆规作⊙O,使它经过A、B、D三点(保留作图痕迹);
(2)点C是否在⊙O上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
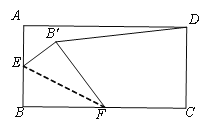
【题目】如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
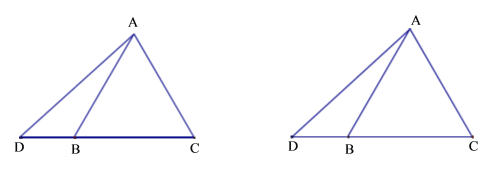
【题目】如图,在等边△ABC中,点D 是边CB延长线上一动点(BD<BC),连接AD,点B 关于直线AD的对称点为E,过D 作DF//AB交CE于点F.
(1)依题意补全图形;
(2)求证:AD=CF;
(3)当∠DCE=15°时,直接写出线段AD,EF,BC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点![]() 是坐标原点,一次函数
是坐标原点,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点.
两点.

(1)求![]() 的值.
的值.
(2)根据图象写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
(3)若一次函数图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,则求出
,则求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
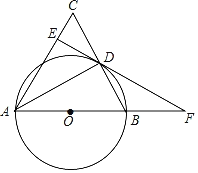
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
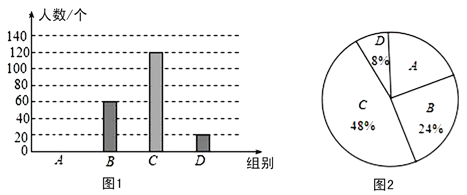
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等边三角形,点D在BC上,BD=2CD,点F是射线AC上的动点,点M是射线AD上的动点,∠AFM=∠DAB,FM的延长线与射线AB交于点E,设AM=x,△AME与△ABD重叠部分的面积为y,y与x的函数图象如图2所示(其中0<x≤m,m<x<n,x≥n时,函数的解析式不同).
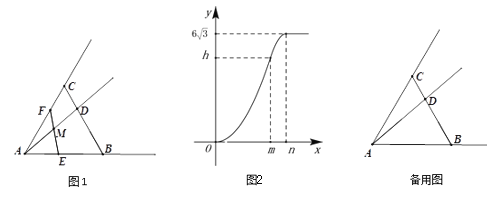
(1)填空:AB=_______;
(2)求出y与x的函数关系式,并求出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com