
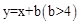 与x轴、y轴分别相交于点A、B,与正比例函数
与x轴、y轴分别相交于点A、B,与正比例函数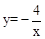 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。 与⊙O有哪些位置关系?求出相应b的取值范围。
与⊙O有哪些位置关系?求出相应b的取值范围。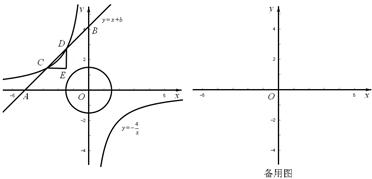
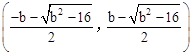 ;
;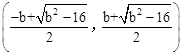 。(2)
。(2)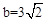 时,点E在⊙O上(3)见解析
时,点E在⊙O上(3)见解析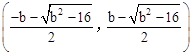 ;
;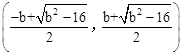 。
。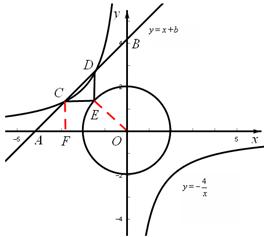
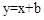 与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,
与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,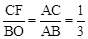 。∴
。∴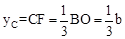 。
。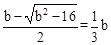 ,解得
,解得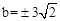 。
。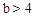 ,∴
,∴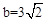 。
。 时,点E在⊙O上。
时,点E在⊙O上。 相切于点G时,
相切于点G时,
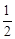 CD=
CD=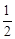 OG=
OG=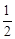 AG。∴AC=CG=GD=DB。∴AC=
AG。∴AC=CG=GD=DB。∴AC=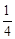 AB。
AB。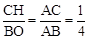 。∴
。∴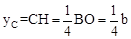 。
。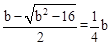 ,解得
,解得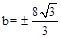 。
。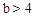 ,∴
,∴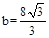 。
。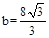 时,直线
时,直线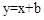 与⊙O相切;
与⊙O相切;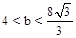 时,直线
时,直线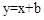 与⊙O相离;
与⊙O相离;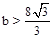 时,直线
时,直线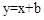 与⊙O相交。
与⊙O相交。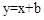 与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,
与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,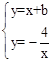 得,
得,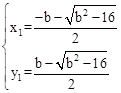 或
或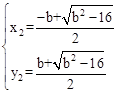 。
。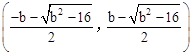 ,点D的坐标为
,点D的坐标为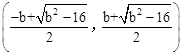 。
。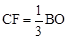 ,代入CF、BO关于b的关系式求解即得所求。
,代入CF、BO关于b的关系式求解即得所求。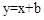 与⊙O相切时,b的取值即可得到直线
与⊙O相切时,b的取值即可得到直线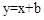 与⊙O的位置关系。
与⊙O的位置关系。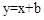 相切于点G时,连接OG,过点C作CH⊥x轴于点H。由整个图形是轴对称图形,可求得AC=CG=GD=DB,即AC=
相切于点G时,连接OG,过点C作CH⊥x轴于点H。由整个图形是轴对称图形,可求得AC=CG=GD=DB,即AC=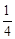 AB。由△AHC∽△AOB可求得
AB。由△AHC∽△AOB可求得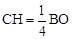 ,代入CH、BO关于b的关系式求解即得⊙O与直线
,代入CH、BO关于b的关系式求解即得⊙O与直线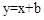 相切时相应b的值。从而得到直线
相切时相应b的值。从而得到直线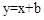 与⊙O相离和相交时相应b的取值范围。
与⊙O相离和相交时相应b的取值范围。

科目:初中数学 来源:不详 题型:解答题
 ,sin∠BCP=
,sin∠BCP=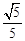 ,求点B到AC的距离.
,求点B到AC的距离.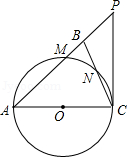
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
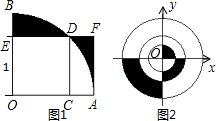
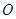 ,大圆的弦
,大圆的弦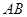 切小圆于
切小圆于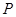 ,两圆的半径分别为
,两圆的半径分别为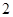 和
和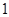 ,则弦长
,则弦长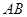 = ;若用阴影部分围成一个圆锥,则该圆锥的底面半径为 .(结果保留根号)
= ;若用阴影部分围成一个圆锥,则该圆锥的底面半径为 .(结果保留根号)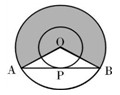
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com