
【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地,甲车以
地,甲车以![]() 的速度行驶
的速度行驶![]() 后,乙车才沿相同路线行驶,乙车先到达
后,乙车才沿相同路线行驶,乙车先到达![]() 地并停留
地并停留![]() 后,再以原速沿原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速沿原路返回,直至与甲车相遇.在此过程中,两车之间的距离![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数关系如图所示,下列说法错误的是( )
之间的函数关系如图所示,下列说法错误的是( )
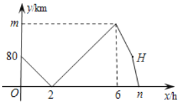
A.乙车的速度是![]() B.
B.![]()
C.点![]() 的坐标是
的坐标是![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
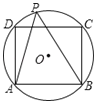
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了![]() 条口罩生产线,每条生产线每天可生产口罩
条口罩生产线,每条生产线每天可生产口罩![]() 个.如果每增加一条生产线,每条生产线就会比原来少生产
个.如果每增加一条生产线,每条生产线就会比原来少生产![]() 个口罩.设增加
个口罩.设增加![]() 条生产线后,每条生产线每天可生产口罩
条生产线后,每条生产线每天可生产口罩![]() 个.
个.
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 若每天共生产口罩
若每天共生产口罩![]() 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?
个,在投入人力物力尽可能少的情况下,应该增加几条生产线?
![]() 设该厂每天可以生产的口罩
设该厂每天可以生产的口罩![]() 个,请求出
个,请求出![]() 与
与![]() 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
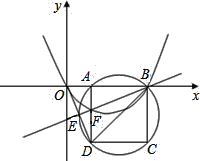
【题目】如图,在平面直角坐标系中,已知点![]() 、
、![]() ,以
,以![]() 为边在
为边在![]() 轴下方作正方形
轴下方作正方形![]() ,点
,点![]() 是线段
是线段![]() 与正方形
与正方形![]() 的外接圆的交点,连接
的外接圆的交点,连接![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,试求经过
,试求经过![]() 、
、![]() 、
、![]() 三点的抛物线
三点的抛物线![]() 的解析式;
的解析式;
(3)在(2)的条件下,将抛物线![]() 在
在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新图象,若直线
轴翻折,图象的其余部分保持不变,得到一个新图象,若直线![]() 向上平移t个单位与新图象有两个公共点,试求t的取值范围.
向上平移t个单位与新图象有两个公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
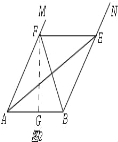
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
小王同学参加某高中学校进行的自主招生考试,本次考试共有1000人参加.
(1)1000人参加自招考试,有300人可以享受加分政策,且有10,20,30,60四个档次,小王想获得至少30分的加分,那么概率为多少?
(2)若该高中的中考录取分数线为530分,小王估得中考分数可能在500-509,510-519,520-529三个分段,
①若小王的中考分数在510~519分段,则小王被该高中录取的概率为多少?
②若小王的中考分数在三个分数段对应的概率分别为![]() ,
,![]() ,
,![]() ,则小王被该高中录取的概率为多少?
,则小王被该高中录取的概率为多少?
加分 | 人数 |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com