

 CE.过E作EH∥BD交CB的延长线于H,容易证明△HCE等腰直角三角形,由此可以得到∠HCE=∠HEC=45°,而根据已知条件可以得到∠FBC=45°,∴∠BGE=∠HCE+∠FBC=90°,这样就可以得到BF⊥CE,然后根据已知条件和勾股定理计算证明BF=
CE.过E作EH∥BD交CB的延长线于H,容易证明△HCE等腰直角三角形,由此可以得到∠HCE=∠HEC=45°,而根据已知条件可以得到∠FBC=45°,∴∠BGE=∠HCE+∠FBC=90°,这样就可以得到BF⊥CE,然后根据已知条件和勾股定理计算证明BF=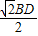 ,CE=
,CE=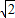 BD,从而证明了BF=
BD,从而证明了BF= CE.从证明过程可以看出无论三角形是等腰直角三角形还是普通直角三角形,对题目的结果没有影响.
CE.从证明过程可以看出无论三角形是等腰直角三角形还是普通直角三角形,对题目的结果没有影响. CE.
CE. CE
CE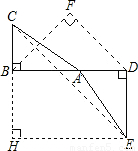
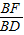
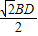
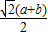
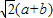
 CE
CE CE
CE

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
 10、如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别与AD、AE相交于点F、G.图中共有n对三角形相似(相似比不等于1),则n的值是( )
10、如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别与AD、AE相交于点F、G.图中共有n对三角形相似(相似比不等于1),则n的值是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 2 |
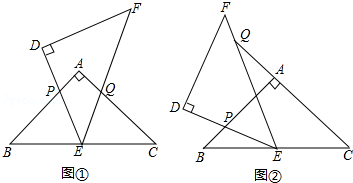
查看答案和解析>>
科目:初中数学 来源: 题型:
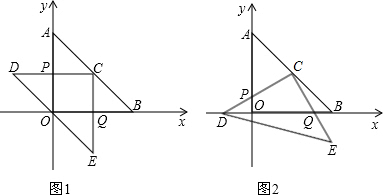
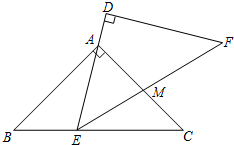 如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com