【题目】计算题
（1）计算：（cos230°+sin230°）×tan60°
（2）解方程：x2﹣2 
x﹣1=0．
【答案】
（1）解：原式=[（ 
）2+（ 
）2]× 
=
（2）解：△=（﹣2 ）2﹣4×（﹣1）
=16，
x= 
= ±2，
所以x1= +2，x2= ﹣2
【解析】（1）将特殊角的三角函数值代入计算即可。
（2）根据一元二次方程的求根公式法解此方程。
【考点精析】通过灵活运用公式法和特殊角的三角函数值，掌握要用公式解方程，首先化成一般式．调整系数随其后，使其成为最简比．确定参数abc，计算方程判别式．判别式值与零比，有无实根便得知．有实根可套公式，没有实根要告之；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”即可以解答此题．
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案科目：初中数学 来源： 题型：
【题目】阅读材料：已知方程a2
2a1=0，12bb2=0且ab≠1，求
的值.
解：由a22a1=0及12bb2=0，
可知a≠0，b≠0，
又∵ab≠1，
.
12bb2=0可变形为
，
根据a22a1=0和的特征.
、
是方程x22x1=0的两个不相等的实数根，
则
，即
.
根据阅读材料所提供的方法，完成下面的解答.
已知：3m27m2=0，2n2+7n3=0且mn≠1，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BE和CE分别为△ABC的内角平分线和外角平分线，BE⊥AC于点H，CF平分∠ACB交BE于点F连接AE．则下列结论：①∠ECF=90°；②AE=CE；③
；④∠BAC=2∠BEC；⑤∠AEH=∠BCF，正确的个数为（ ）
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）
（1）作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1，并写出C1点的坐标 ；
（2）作出△ABC关于原点O成中心对称的△A2B2C2，并求出△ABC的面积 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程．
已知：如图 
，直线 
及直线 外一点 
．
求作：直线 
，使得 
．
作法：如图 
．
①在直线 上取一点 
，连接 
；
②作 
的平分线 
；
③以点 为圆心， 长为半径画弧，交射线 于点 
；
④作直线 ．
所以直线 就是所求作的直线．根据小明设计的尺规作图过程．
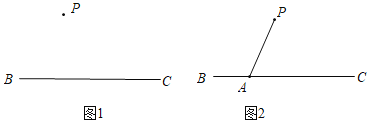
（1）使用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：
平分 ，
．
，
，
，
（____________________）（填推理依据）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起（其中，
，
；
）．
（1）①若
，则
的度数为_____________；
②若
，则
的度数为_____________．
（2）由（1）猜想与的数量关系，并说明理由．
（3）当
且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请写出
角度所有可能的值（不必说明理由）；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，∠BAC=45°，BC=2，D是线段BC上的一个动点，点D是关于直线AB、AC的对称点分别为M、N，则线段MN长的最小值是 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点C，D在AB同侧，∠CAB=∠DBA，下列条件中不能判定△ABD≌△BAC的是（ ）
A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
