
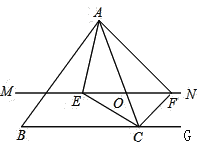
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
【答案】(1)详见解析;(2)当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,理由详见解析;(3)当点
是矩形,理由详见解析;(3)当点![]() 运动到
运动到![]() 的中点时,且
的中点时,且![]() 满足
满足![]() 为直角的直角三角形时,四边形
为直角的直角三角形时,四边形![]() 是正方形,理由详见解析.
是正方形,理由详见解析.
【解析】
(1)由平行线的性质和角平分线的定义得出![]() ,
,![]() , 得出
, 得出![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(2)先证明四边形![]() 是平行四边形,再由对角线相等,即可得出结论;
是平行四边形,再由对角线相等,即可得出结论;
(3)由正方形的性质得出![]() ,得出
,得出![]() 即可.
即可.
(1)![]() ,
,
![]() ,
,
又![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
同理:![]() ,
,
![]() .
.
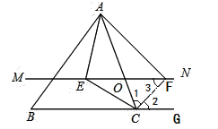
(2)当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形.
是矩形.
![]() 当点
当点![]() 运动到
运动到![]() 的中点时,
的中点时,![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
由(1)可知,![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 四边形
四边形![]() 是矩形.
是矩形.
(3)当点![]() 运动到
运动到![]() 的中点时,且
的中点时,且![]() 满足
满足![]() 为直角的直角三角形时,四边形
为直角的直角三角形时,四边形![]() 是正方形.
是正方形.
![]() 由(2)知,当点
由(2)知,当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,
是矩形,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形.
是正方形.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,直线AB//CD,试确定∠B,∠BPC,∠C之间的数量关系:
(2)如图②,直线AB//CD.∠ABP与∠DCP的平分线相交于点P1,请确定∠P与∠P1的数量关系;
(3)如图③,若∠A=![]() (0<
(0<![]() <180°,且
<180°,且![]() ≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线
≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线![]() 和
和![]() .使得,
.使得,![]() 、
、![]() 分别与AB,AC的夹角为
分别与AB,AC的夹角为![]() .且
.且![]() 和
和![]() 交于点O,请直接写出∠BOC的度数.
交于点O,请直接写出∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小李从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2m,现己知购买这种铁皮每平方米需30元钱,问小李购回这张矩形铁皮共花了多少元钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
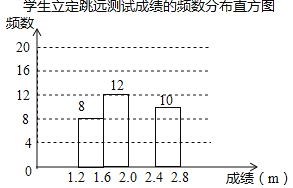
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
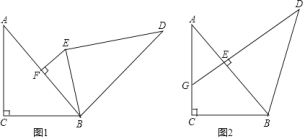
【题目】已知:把![]() 和
和![]() 按如图甲摆放(点
按如图甲摆放(点![]() 与点
与点![]() 重合),点
重合),点![]() 、
、![]() 、
、![]() 在同一条直线上.
在同一条直线上.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如图乙,
.如图乙,![]() 从图甲的位置出发,以
从图甲的位置出发,以![]() 的速度沿
的速度沿![]() 向
向![]() 匀速移动,在
匀速移动,在![]() 移动的同时,点
移动的同时,点![]() 从
从![]() 的顶点
的顶点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动.当点
匀速移动.当点![]() 移动到点
移动到点![]() 时,
时,![]() 点停止移动,
点停止移动,![]() 也随之停止移动.
也随之停止移动.![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() .解答下列问题:
.解答下列问题:
![]() 设三角形
设三角形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 当
当![]() 为何值时,三角形
为何值时,三角形![]() 为等腰三角形?
为等腰三角形?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使
,使![]() 、
、![]() 、
、![]() 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 旋转一定的角度,得到
旋转一定的角度,得到![]() .
.
(1)若点![]() 为
为![]() 边上中点,连接
边上中点,连接![]() ,则线段
,则线段![]() 的范围为________.
的范围为________.
(2)如图![]() ,当
,当![]() 直角顶点
直角顶点![]() 在
在![]() 边上时,延长
边上时,延长![]() ,交
,交![]() 边于点
边于点![]() ,请问线段
,请问线段![]() 、
、![]() 、
、![]() 具有怎样的数量关系,请写出探索过程.
具有怎样的数量关系,请写出探索过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB 是⊙O的直径,弦CD⊥AB于点H,点M是弧CBD 上任意一点,AH=2,CH=4.
(1)求⊙O 的半径r 的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O 于点 N,连接BN交CE于点 F,求HE![]() HF的值.
HF的值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com