
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为斜边
为斜边![]() 上的一个动点,则
上的一个动点,则![]() 的最小值为__________.
的最小值为__________.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.

(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG 的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习了整式的乘法,两个多项式相乘,我们可以运用法则,将其展开,例如:![]() ,而将等号的左右两边互换,我们得到了
,而将等号的左右两边互换,我们得到了![]() ,等号的左边是一个多项式,而右边是几个整式相乘的形式,我们规定将一个多项式写成几个整式相乘的形式,这种运算称之为“因式分解”
,等号的左边是一个多项式,而右边是几个整式相乘的形式,我们规定将一个多项式写成几个整式相乘的形式,这种运算称之为“因式分解”
问题提出:
如何将![]() 进行因式分解呢?
进行因式分解呢?
问题探究:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释
例如:我们可以通过表示几何图形面积的方法来快速的对多项式![]() 进行因式分解.
进行因式分解.
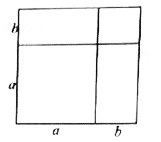
如图所示边长为![]() 的大正方形是由1个边长为
的大正方形是由1个边长为![]() 的正方形,2个边长为
的正方形,2个边长为![]() 的长方形,1个边长为
的长方形,1个边长为![]() 的正方形,
的正方形,![]() 组成,我们可以用两种方法表示大正方形的面积,这个图形的面积可以表示成:
组成,我们可以用两种方法表示大正方形的面积,这个图形的面积可以表示成:![]() 或
或![]()
∴![]()
我们将等号左边的多项式写成了右边两个整式相乘的形式,从而成功的对多项式![]() 进行了因式分解
进行了因式分解
请你类比上述方法,利用图形的几何意义对多项式![]() 进行因式分解(要求自己构图并写出推证过程)
进行因式分解(要求自己构图并写出推证过程)
问题拓展:
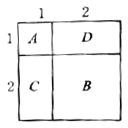
如何利用图形几何意义的方法推导:![]() ?如图,
?如图,![]() 表示1个
表示1个![]() 的正方形,即
的正方形,即![]() ,
,![]() 表示1个
表示1个![]() 的正方形,
的正方形,![]() 与
与![]() 恰好可以拼成1个
恰好可以拼成1个![]() 的正方形,因此:
的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个
就可以表示2个![]() 的正方形,即
的正方形,即![]() ,而
,而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.由此可得:
的大正方形.由此可得:![]()
尝试解决:
请你类比上述推导过程,利用图形几何意义方法推导出![]() 的值.
的值.
(要求自己构造图形并写出推证过程).
解:
归纳猜想:![]() _________________.
_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社组织一批游客外出旅游,原计划租用30座客车若干辆,但有15人没有座位;若租用同样数量的45座客车,则多出一辆车,且其余客车恰好坐满。已知30座客车租金为每辆220元,45座客车租金为每辆300元,问:
(1)这批游客的总人数是多少?原计划租用多少辆30座客车?
(2)若租用同一种客车,要使每位游客都有座位,应该怎样租用才合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把
,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把![]() 沿EF折叠,点B落在点
沿EF折叠,点B落在点![]() 处.若
处.若![]() ,当
,当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为__________.
的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
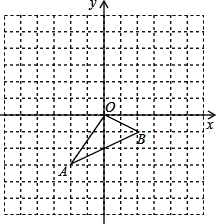
【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
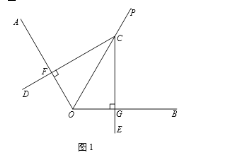
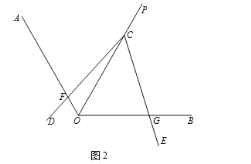
【题目】已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com