
【题目】如图①,直线CD与以线段OB为直径的半⊙A相切于点C,连接OC、BC,作OD⊥CD,垂足为D,OB=10,
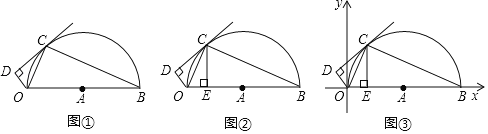
(1)求证:∠OCD=∠OBC;
(2)如图②,作CE⊥OB于点E,若CE=AE,求线段OD的长;
(3)如图③,在(2)的条件下,以O点为原点建立平面直角坐标系求△DOB外接圆的圆心坐标.
以下是优优和乐乐两位同学对第(3)小题的讨论
优优:这题很简单嘛,我只要求出这个三角形任意两条边的中垂线解析式,然后求交点坐标就行了.乐乐:我还有其他的好方法.
如果你是乐乐,你会怎么做?
【答案】(1)证明见解析;(2)5﹣![]() ;(3)△DOB外接圆的圆心坐标为(5,
;(3)△DOB外接圆的圆心坐标为(5,![]() )
)
【解析】
(1)连接OC,由题意可得∠OBC+∠COB=90°,∠ACO+∠DCO=90°,由AC=OA,可得∠ACO=∠AOC,即可证∠OCD=∠OBC;
(2)连接CA,由题意可证△CDO≌△CEO,可得OD=OE,由OA=AB=AC=5,CE=AE,CE⊥OB,可得AE=![]() ,即可求OD的长;
,即可求OD的长;
(3)设直线CD与x轴交于点N,过点B作BM⊥x轴交直线CD于点M,连接AC,OM,由题意可求∠CAE=∠ACE=45°=∠CNA=∠CMB,可得AC=CN,BM=BN,根据勾股定理可求AN的长,即可求BM的长,可得点M坐标,由∠MDO=∠MBO=90°,可证点D,点O,点B,点M四点共圆,即OM是直径,则OM的中点是圆心,也是△DOB外接圆的圆心,根据中点坐标公式可求OM中点坐标.
解:(1)如图:连接OC
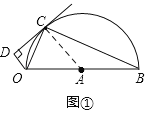
∵OB是直径
∴∠OCB=90°
∴∠OBC+∠COB=90°
∵CD是⊙A的切线
∴AC⊥CD
∴∠ACO+∠DCO=90°
∵AC=OA
∴∠ACO=∠AOC
∴∠OCD=∠OBC;
(2)如图:连接CA
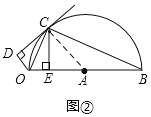
∵CE⊥OB
∴∠COB+∠OCE=90°且∠OBC+∠COB=90°
∴∠OCE=∠OBC且∠OCD=∠OBC
∴∠OCD=∠OCE且OC=OC,∠CDO=∠CEO=90°
∴△CDO≌△CEO(AAS)
∴OD=OE
∵OB=10,
∴OA=AB=AC=5
∵CE=AE,CE⊥OB
∴AE2+CE2=AC2.
∴AE=![]() =CE
=CE
∴OE=5﹣![]() =OD
=OD
(3)如图:设直线CD与x轴交于点N,过点B作BM⊥x轴交直线CD于点M,连接AC,OM
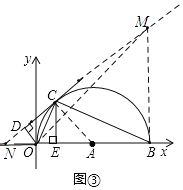
∵CE=AE,CE⊥OB
∴∠CAE=∠ACE=45°,
又∵AC⊥CD
∴∠CNA=∠CAE=45°
∴AC=CN=5
∴AN=![]() =5
=5![]()
∵BN=AN+AB
∴BN=5![]() +5
+5
∵BM⊥AB,∠CNA=45°
∴∠CNA=∠CMB=45°
∴BN=BM=5![]() +5,且OB=10
+5,且OB=10
∴点M的坐标为(10,5![]() +5)
+5)
∵∠MDO=∠MBO=90°
∴点D,点O,点B,点M四点共圆
∴OM是直径
∴OM的中点是圆心,也是△DOB外接圆的圆心;
∵点O(0,0),点M(10,5![]() +5)
+5)
∴△DOB外接圆的圆心坐标为(5,![]() )
)


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
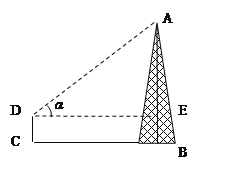
【题目】如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)
(参考数据:sin43° =0.6820, cos43° =0.7314, tan43° =0.9325
查看答案和解析>>
科目:初中数学 来源: 题型:
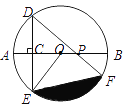
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场老板准备建造一个矩形羊圈![]() ,他打算让矩形羊圈的一面完全靠着墙
,他打算让矩形羊圈的一面完全靠着墙![]() ,墙
,墙![]() 可利用的长度为
可利用的长度为![]() ,另外三面用长度为
,另外三面用长度为![]() 的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)

![]() 若要使矩形羊圈的面积为
若要使矩形羊圈的面积为![]() ,则垂直于墙的一边长
,则垂直于墙的一边长![]() 为多少米?
为多少米?
![]() 农场老板又想将羊圈
农场老板又想将羊圈![]() 的面积重新建造成面积为
的面积重新建造成面积为![]() ,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
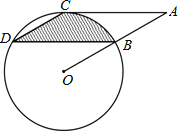
【题目】如图,点B、C、D都在![]() 上,过点C作
上,过点C作![]() 交OB延长线于点A,连接CD,且
交OB延长线于点A,连接CD,且![]() ,
,![]() .
.
(1)直线AC与![]() 有怎样的位置关系?为什么?
有怎样的位置关系?为什么?
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
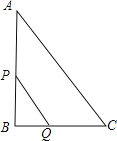
【题目】如图,Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连接PQ.设动点运动时间为x秒.
(1)用含x的代数式表示BQ、PB的长度;
(2)当x为何值时,△PBQ为等腰三角形;
(3)是否存在x的值,使得四边形APQC的面积等于20cm2?若存在,请求出此时x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
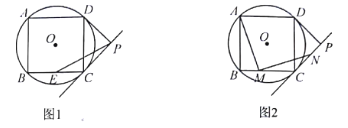
【题目】如图,四边形![]() 是
是![]() 的内接正方形,
的内接正方形,![]() ,
,![]() 、
、![]() 是
是![]() 的两 条切线,
的两 条切线,![]() 、
、![]() 为切点.
为切点.
(1)如图1,求![]() 的半径;
的半径;
(2)如图1,若点![]() 是
是![]() 的中点,连结
的中点,连结![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,若点![]() 是
是![]() 边上任意一点(不含
边上任意一点(不含![]() 、
、![]() ),以点
),以点![]() 为直角顶点,在
为直角顶点,在![]() 的上方作
的上方作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com