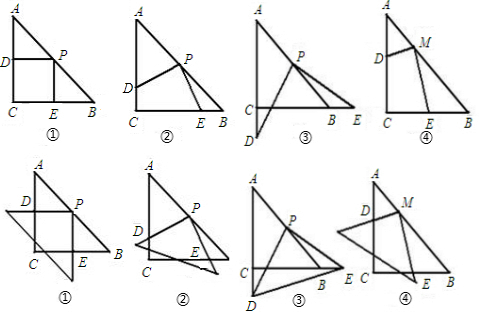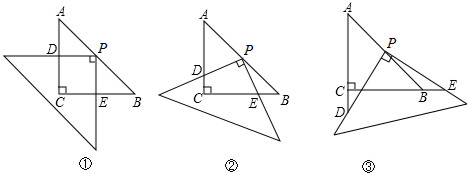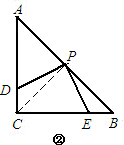
解:(1)PD=PE依然成立.
证明:连接PC,∵△ABC是等腰直角三角形,P是AB中点,
∴CP=PB,CP⊥AB,∠ACP=

∠ACB=45°,
即∠ACP=∠B=45°
∵∠DPC+∠CPE=∠BPE+∠CPE=90°,
∴∠DPC=∠BPE,
∴△PCD≌△PBE,
∴PD=PE.
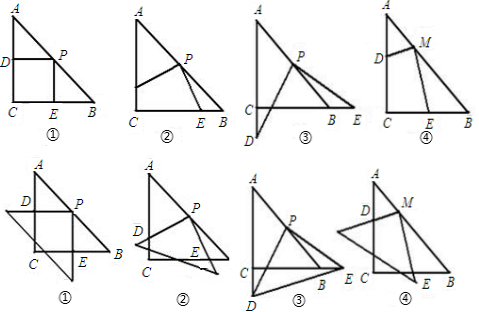
(2)分三种情况讨论如下:
①当PE=PB,点C与点E重合,即CE=0.
②当PE=BE时,CE=1.
③当BE=PB时
若点E在线段CB上时,CE=
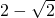
,
若点E在CB延长线上时
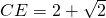
.
(3)过点M作MF⊥AC,MH⊥BC.
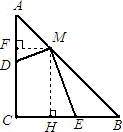
∵∠C=90°,
∴四边形CFMH是矩形即∠FMH=90°,MF=CH.
∵
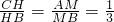
而HB=MH,
∴

∵∠DMF+∠DMH=∠DMH+∠EMH=90°,
∴∠DMF=∠EMH,
∵∠MFD=∠MHE=90°,
∴△MFD∽△MHE,
即
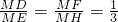
.
分析:(1)因为△ABC是等腰直角三角形,所以连接PC,容易得到△ACP、△CPB都是等腰直角三角形.连接CP,就可以证明△CDP≌△BEP,再根据全等三角形的对应边相等,就可以证明DP=PE;
(2)△PBE能成为等腰三角形,位置有四种;
(3)作MH⊥CB,MF⊥AC,构造相似三角形△MDF和△MHE,然后利用对应边成比例,就可以求出MD和ME之间的数量关系.
点评:此题比较复杂,综合考查全等三角形的判定与性质、相似三角形的判定与性质、矩形的判定与性质、图形的变换.综合性很强,勾股定理的计算要求也比较高.

 解:(1)PD=PE依然成立.
解:(1)PD=PE依然成立. ∠ACB=45°,
∠ACB=45°,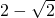 ,
,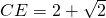 .
.
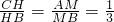 而HB=MH,
而HB=MH,
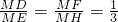 .
.