
已知⊙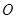 的半径为1,以
的半径为1,以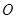 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形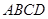 ,顶点
,顶点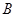 的坐标为(
的坐标为(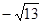 ,0),顶点
,0),顶点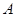 在
在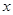 轴上方,顶点
轴上方,顶点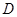 在⊙
在⊙ 上运动.
上运动.
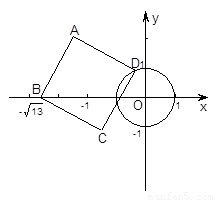
(1)当点 运动到与点
运动到与点 、
、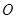 在一条直线上时,
在一条直线上时,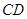 与⊙
与⊙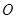 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出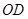 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由;
(2)设点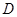 的横坐标为
的横坐标为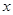 ,正方形
,正方形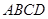 的面积为
的面积为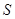 ,求出
,求出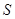 与
与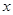 的函数关系式,并求出
的函数关系式,并求出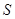 的最大值和最小值.
的最大值和最小值.
(1)CD与⊙O相切
(2)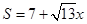 ,S的最大值为
,S的最大值为 ,S的最小值为
,S的最小值为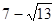
【解析】
试题分析:(1)因为A、D、O在一直线上,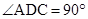 ,
,
所以∠COD=90°,所以CD是⊙O的切线
CD与⊙O相切时,有两种情况:
① 点在第二象限时(如图①),
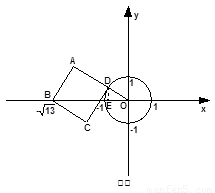
设正方形ABCD的边长为a,
则 ,
,
解得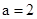 ,或
,或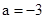 (舍去)
(舍去)
过点D作DE⊥OB于E,则Rt△ODE≌Rt△OBA,
所以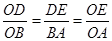 ,
,
所以DE=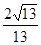 ,OE=
,OE=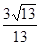 ,
,
所以点D1的坐标是(-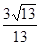 ,
,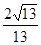 )
)
所以OD所在直线对应的函数表达式为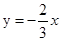
②切点在第四象限时(如图②),
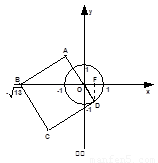
设正方形ABCD的边长为b,则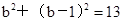 ,
,
解得 (舍去),或
(舍去),或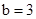
过点D作DF⊥OB于F,则Rt△ODF∽Rt△OBA,
所以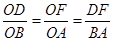 ,
,
所以OF=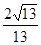 ,DF=
,DF=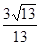 ,
,
所以点D2的坐标是(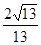 ,-
,-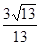 )
)
所以OD所在直线对应的函数表达式为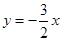
(2)过点D作DG⊥OB于G,连接BD、OD,
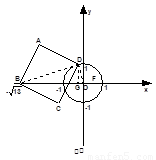
则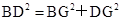
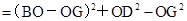
=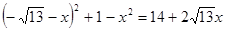
所以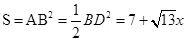
因为 ,所以S的最大值为
,所以S的最大值为 ,
,
S的最小值为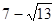
考点:函数图象与几何的结合
点评:作为试卷的压轴题,难度一般都不小,此类题目,只能通过多做多练,寻找其中的规律


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
 |
| AB |
 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2| 3 |
| AD |
| DC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系.有一个正方形ABCD,顶点B的坐标为(-
已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系.有一个正方形ABCD,顶点B的坐标为(-| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AOB |
 |
| BCA |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com