
【题目】已知![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,一条直线
,一条直线![]() 与边
与边![]() 相交于点
相交于点![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
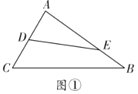
(1)如图①,若![]() 将
将![]() 分成周长相等的两部分,求
分成周长相等的两部分,求![]() 的值;(用
的值;(用![]() 、
、![]() 、
、![]() 表示)
表示)
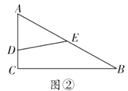
(2)如图②,若![]() ,
,![]() ,
,![]() ,
,![]() 将
将![]() 分成周长、面积相等的两部分,求
分成周长、面积相等的两部分,求![]() 的值;
的值;
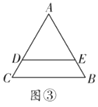
(3)如图③,若![]() 将
将![]() 分成周长、面积相等的两部分,且
分成周长、面积相等的两部分,且![]() ,则
,则![]() 、
、![]() 、
、![]() 满足什么关系?
满足什么关系?
科目:初中数学 来源: 题型:
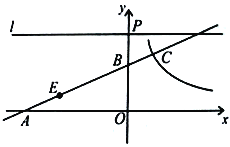
【题目】已知:如图,直线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,线段
,线段![]() 的长是方程
的长是方程![]() 的一个根,请解答下列问题:
的一个根,请解答下列问题:
(1)求点![]() 的坐标;
的坐标;
(2)双曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,
上,![]() ,直线
,直线![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 上的坐标平面内是否存在点
上的坐标平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请求出点
为顶点的四边形是矩形?若存在,请求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两组卡片共5张,
两组卡片共5张,![]() 组中三张分别写有数字2、4、6,
组中三张分别写有数字2、4、6,![]() 组中两张分别写有数字3、5,它们除数字外其他都相同.
组中两张分别写有数字3、5,它们除数字外其他都相同.
(1)随机从![]() 组中抽取一张,则抽到数字是2的概率为______;
组中抽取一张,则抽到数字是2的概率为______;
(2)分别随机从![]() 组、
组、![]() 组中各抽取一张.现制定这样一个游戏规则:若所抽取的两个数字之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?请你用画树状图或列表的方法计算并说明理由.
组中各抽取一张.现制定这样一个游戏规则:若所抽取的两个数字之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?请你用画树状图或列表的方法计算并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点M,N在同一个正比例函数图象上的是( )
A.M(2,﹣3),N(﹣4,6)B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)D.M(2,3),N(﹣4,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
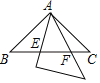
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
A.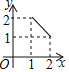 B.
B.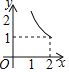 C.
C.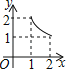 D.
D.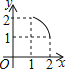
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个周末小月和小华在南滨路跑步锻炼身体,两人同时从A点出发,沿直线跑到B点后马上掉头原路返回A点算一个来回,回到A点后又马上调头去往B点,以此类推,每人要完成2个来回。一直两人全程均保持匀速,掉头时间忽略不计。如图所示是小华从出发到他率先完成第一个来回为止,两人到B点的距离之和y(米)与小华跑步时间x(分钟)之间的函数图像,则当小华跑完2个来回时,小月离B点的距离为___米.
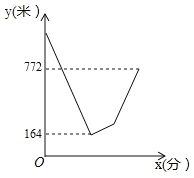
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为□ABCD中一点,EA=ED,∠AED=90,点F,G分别为AB,BC上的点,连接DF,AG,AD=AG=DF,且AG⊥DF于点H,连接EG,DG,延长AB,DG相交于点P.
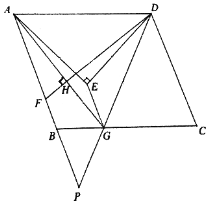
(1)若AH=6,FH=2,求AE的长;
(2)求证:∠P=45;
(3)若DG=2PG,求证:∠AGE=∠EDG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
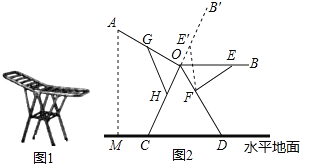
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
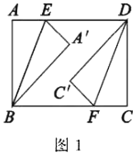
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,且
边上,且![]() ,连接
,连接![]() ,
,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折叠,点
折叠,点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处.
处.
探究展示:
(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .(依据1)
.(依据1)
∴![]() .
.
∴![]() .(依据2)
.(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:
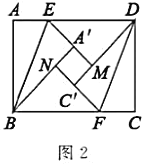
(2)如图2,折叠过程中,当点![]() ,
,![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
联想拓广:
(3)如图3,连接![]() ,
,![]() ,
,![]() .
.

①当![]() 时,
时,![]() 的长为________;
的长为________;
②![]() 的长有最大值吗?若有,请你直接写出
的长有最大值吗?若有,请你直接写出![]() 长的最大值和此时四边形
长的最大值和此时四边形![]() 的形状;若没有,请说明理由.
的形状;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com