
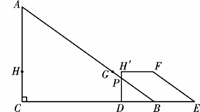
如图11,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,DEF=∠CBA,AH∶AC=2∶3
(1)延长HF交AB于G,求△AHG的面积.
(2)操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停止,设运动的时间为t秒,运动后的直角梯形为DEFH′(如图12).
探究1:在运动中,四边形CDH′H能否为正方形?若能, 请求出此时t的值;若不能,请说明理由.
探究2:在运动过程中,△ABC与直角梯形DEFH′重叠部分的面积为y,求y与t的函数关系.
解:(1)∵AH∶AC=2∶3,AC=6
∴AH=![]() AC=
AC=![]() ×6=4
×6=4
又∵HF∥DE,∴HG∥CB,∴△AHG∽△ACB
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴HG=
,∴HG=![]()
∴S△AHG=![]() AH?HG=
AH?HG=![]() ×4×
×4×![]() =
=![]()
(2)①能为正方形
∵HH′∥CD,HC∥H′D,∴四边形CDH′H为平行四边形
又∠C=90°,∴四边形CDH′H为矩形
又CH=AC-AH=6-4=2
∴当CD=CH=2时,四边形CDH′H为正方形
此时可得t=2秒时,四边形CDH′H为正方形
②(Ⅰ)∵∠DEF=∠ABC,∴EF∥AB
∴当t=4秒时,直角梯形的腰EF与BA重合.
当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积.
过F作FM⊥DE于M,![]() =tan∠DEF=tan∠ABC=
=tan∠DEF=tan∠ABC=![]() =
=![]() =
=![]()
∴ME=![]() FM=
FM=![]() ×2=
×2=![]() ,HF=DM=DE-ME=4-
,HF=DM=DE-ME=4-![]() =
=![]()
∴直角梯形DEFH′的面积为![]() (4+
(4+![]() )×2=
)×2=![]()
∴y=![]()
(Ⅱ)∵当4<t≤5![]() 时,重叠部分的面积为四边形CBGH的面积-矩形CDH′H的面积.
时,重叠部分的面积为四边形CBGH的面积-矩形CDH′H的面积.
而S边形CBGH=S△ABC-S△AHG=![]() ×8×6-
×8×6-![]() =
=![]()
 S矩形CDH′H=2t
S矩形CDH′H=2t
∴y=![]() -2t
-2t
(Ⅲ)当5![]() <t≤8时,如图,设H′D交AB于P.
<t≤8时,如图,设H′D交AB于P.
BD=8-t
又![]() =tan∠ABC=
=tan∠ABC=![]()
∴PD=![]() DB=
DB=![]() (8-t)1 ∴重叠部分的面积y=S
(8-t)1 ∴重叠部分的面积y=S
△PDB=![]() PD?DB
PD?DB
=![]() ?
?![]() (8-t)(8-t)
(8-t)(8-t)
=![]() (8-t)2=
(8-t)2=![]() t2-6t+24
t2-6t+24
∴重叠部分面积y与t的函数关系式:
![]() y=
y=![]() (0≤t≤4)
(0≤t≤4)
![]() -2t(4<t≤5
-2t(4<t≤5![]() )
)
![]() t2-6t+24(5
t2-6t+24(5![]() <t≤8)
<t≤8)
(注:评分时,考生未作结论不扣分)


科目:初中数学 来源: 题型:
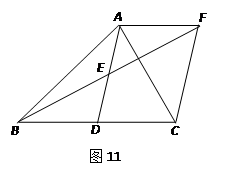
(满分11分)如图11,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连结CF.
(1)求证:AF=CD;
(2)若AB=AC,∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,求sin∠ABF的值.
 |
查看答案和解析>>
科目:初中数学 来源:2011年海南省海口市初三学业模拟考试数学卷 题型:解答题
(满分11分)如图11,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连结CF.
(1)求证:AF=CD;
(2)若AB=AC,∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,求sin∠ABF的值.
 |
查看答案和解析>>
科目:初中数学 来源:2013届江苏苏州星港学校八年级下5月月考数学试卷(解析版) 题型:填空题
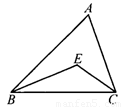
如图11,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°,则∠BEC=______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com