
如图,已知直线 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.

(1)求证:
 ∽
∽ ;
;
(2)如果圆M的半径为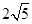 ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;
(3)在(2)的条件下,试问此抛物线上是否存在点P,使得以P、A、M三点为顶点的三角形与 相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
(1)略
(2)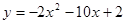
(3)见解析
【解析】(1)略
(2)A(0,12),B(6,0),AB=6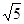
由△ADM∽△AOB得:
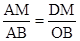 即
即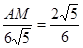
∴AM=10
∴M(0,2)
抛物线解析式为: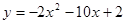
(3)由题已知:△PAM与△ADM相似
①当∠PAM=90°时,此时△PAM与△ADM不相似,这样的点P不存在
②当∠P1MA=90°时,则点P纵坐标为2,由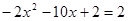 得
得
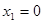 (舍)
(舍)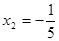 ,此时△PAM∽△BAO,P1(-5,2)
,此时△PAM∽△BAO,P1(-5,2)
③过点M作MP2∥AB交抛物线于P2,则P2(-4,10),此时∠AP2M=90°,
△AP2M∽△MDA
作点D关于 轴对称点P3,其坐标为:(-4,4),此时△AP3M∽△ADM,但点P3不在一抛物线上
轴对称点P3,其坐标为:(-4,4),此时△AP3M∽△ADM,但点P3不在一抛物线上
故P(-4,10),(-5,2)


 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:
 (2013•资阳)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=
(2013•资阳)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=| a | x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
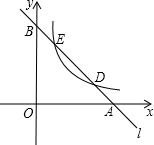 如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=
如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y= (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线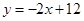 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
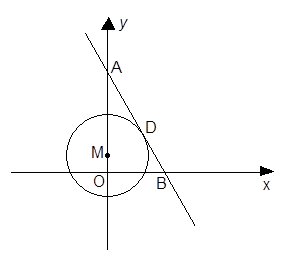
(1)求证:![]()
![]() ∽
∽![]() ;
;
(2)如果圆M的半径为![]() ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以![]() 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;
(3)在(2)的条件下,试问此抛物线上是否存在点P,使得以P、A、M三点为顶点的三角形与![]() 相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
(2013年四川资阳9分)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.

(1)若点D的坐标为(4,1),点E的坐标为(1,4):
①分别求出直线l与双曲线的解析式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com