【题目】在直角坐标系中，点M，N在同一个正比例函数图象上的是（ ）
A.M（2，﹣3），N（﹣4，6）B.M（﹣2，3），N（4，6）
C.M（﹣2，﹣3），N（4，﹣6）D.M（2，3），N（﹣4，6）
【答案】A
【解析】
设正比例函数的解析式为y=kx，根据4个选项中得点M的坐标求出k的值，再代入N点的坐标去验证点N是否在正比例函数图象上，由此即可得出结论．
解：设正比例函数的解析式为y=kx，
A、﹣3=2k，解得：k=
，﹣4×（）=6，6=6，∴点N在正比例函数y=x的图象上；
B、3=﹣2k，解得：k=，4×（）=﹣6，﹣6≠6，∴点N不在正比例函数y=x的图象上；
C、﹣3=﹣2k，解得：k=
，4×=6，6≠﹣6，∴点N不在正比例函数y=x的图象上；
D、3=2k，解得：k=，﹣4×=﹣6，﹣6≠6，∴点N不在正比例函数y=x的图象上．
故选A．
“点睛”本题考查了一次函数图象上点的坐标以及待定系数法求函数解析式，解题的关键是
验证4个选项中点M、N是否在同一个正比例函数图象上. 本题属于基础题，难度不大，解决该题型题目时，根据给定的一点的坐标利用待定系数法求出正比例函数解析式，再代入另一点坐标去验证该点是否在该正比例函数图象上.
小学夺冠AB卷系列答案
ABC考王全优卷系列答案科目：初中数学 来源： 题型：
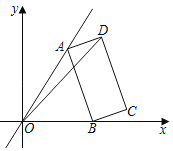
【题目】如图，在平面直角坐标系中，点A在一次函数y＝
x位于第一象限的图象上运动，点B在x轴正半轴上运动，在AB右侧以它为边作矩形ABCD，且AB＝2，AD＝1，则OD的最大值是（ ）
A.
B.
+2C.
+2D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法不正确的是（ ）
A.了解全市中学生对社会主义核心价值观的知晓度的情况，适合用抽样调查
B.若甲组数据方差S2甲＝0.39，乙组数据方差S2乙＝0.27，则乙组数据比甲组数据稳定
C.某种彩票中奖的概率是
，买100张该种彩票一定会中奖
D.旅客上飞机前的安检应该进行全面调查
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题：探究函数y＝x+
的图象和性质．
小华根据学习函数的方法和经验，进行了如下探究，下面是小华的探究过程，请补充完整：
（1）函数的自变量x的取值范围是：____；
（2）如表是y与x的几组对应值，请将表格补充完整：
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
（3）如图，在平面直角坐标系中描点并画出此函数的图象；
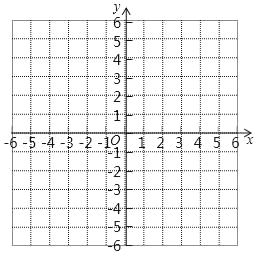
（4）进一步探究：结合函数的图象，写出此函数的性质（一条即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
经过点
，现将抛物线
沿
轴翻折，并向左平移1个单位长度后得到物线
．
（1）求抛物线的解析式．
（2）若抛物线与轴交于
，
两点（点在点右侧），点
在抛物线对称轴上一点，
为坐标原点，则抛物线上是否存在点
，使以，，，为顶点的四边形是干行四边形？若存在，求出点的坐标：若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
，
、
、
的对边分别是
、
、
，一条直线
与边
相交于点
，与边
相交于点
．
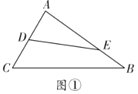
（1）如图①，若将分成周长相等的两部分，求
的值；(用、、表示)
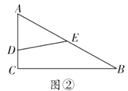
（2）如图②，若
，
，
，将分成周长、面积相等的两部分，求
的值；
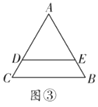
（3）如图③，若将分成周长、面积相等的两部分，且
，则、、满足什么关系？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为迎接县中学生篮球比赛，计划购买A、B两种篮球共20个供学生训练使用．若购买A种篮球6个，则购买两种篮球共需费用720元；若购买A种篮球12个，则购实两种篮球共需费用840元．
（1）A、B两种篮球共需单价各多少元？
（2）设购买A种篮球x个且A种篮球不少于8个，所需费用为y元，试确定y与x的关系式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
