
ЁОЬтФПЁПФГЙЋЫОЩњВњФГжжЩЬЦЗУПМўГЩБОЮЊ20дЊЃЌетжжЩЬЦЗдкЮДРД40ЬьФкЕФШеЯњЪлСПy(Мў)гыЪБМфx(Ьь)ЕФЙиЯЕШчЯТБэЃК
ЪБМфxЃЈЬьЃЉ | 1 | 3 | 6 | 10 | ... |
ШеЯњЪлСПyЃЈМўЃЉ | 94 | 90 | 84 | 76 | ... |
ЮДРД40ЬьФкЃЌЧА20ЬьУПЬьЕФМлИёmЃЈдЊ/МўЃЉгыЪБМфxЃЈЬьЃЉЕФКЏЪ§ЙиЯЕЪНЮЊ![]() (1ЁмxЁм20ЃЉЃЌКѓ20ЬьУПЬьЕФМлИёЮЊ30дЊ/МўЃЈ21ЁмxЁм40ЃЉ.
(1ЁмxЁм20ЃЉЃЌКѓ20ЬьУПЬьЕФМлИёЮЊ30дЊ/МўЃЈ21ЁмxЁм40ЃЉ.
ЃЈ1ЃЉЗжЮіЩЯБэжаЕФЪ§ОнЃЌгУЫљбЇЙ§ЕФвЛДЮКЏЪ§ЁЂЖўДЮКЏЪ§ЁЂЗДБШР§КЏЪ§ЕФжЊЪЖШЗЖЈвЛИіТњзуетаЉЪ§ОнЕФyЃЈМўЃЉгыxЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЃЈ2ЃЉЕБ1ЁмxЁм20ЪБЃЌЩшШеЯњЪлРћШѓЮЊWдЊЃЌЧѓГіWгыxЕФКЏЪ§ЙиЯЕЪН.
ЃЈ3ЃЉдкЮДРД40ЬьжаЃЌФФвЛЬьЕФШеЯњЪлРћШѓзюДѓЃЌзюДѓШеЯњЪлРћШѓЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉy=-2x+96ЃЈ2ЃЉw=![]() ЃЈ3ЃЉЕк14ЬьЪБЃЌЯњЪлРћШѓзюДѓЃЌЮЊ578дЊ
ЃЈ3ЃЉЕк14ЬьЪБЃЌЯњЪлРћШѓзюДѓЃЌЮЊ578дЊ
ЁОНтЮіЁПЃЈ1ЃЉЭЈЙ§ЙлВьБэИёжаЕФЪ§ОнШеЯњЪлСПгыЪБМфtЪЧОљдШМѕЩйЕФЃЌЫљвдШЗЖЈyгыxЪЧвЛДЮКЏЪ§ЙиЯЕЃЛЃЈ2ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіКЏЪ§ЙиЯЕЪНЃЛЃЈ3ЃЉЗжЧА20ЬьКЭКѓ20ЬьЗжБ№ЬжТлЃКИљОнШеЯњЪлСПЁЂУПЬьЕФМлИёМАЪБМфxПЩвдСаГіЯњЪлРћШѓWЙигкxЕФЖўДЮКЏЪ§ЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓГіФФвЛЬьЕФШеЯњЪлРћШѓзюДѓЃЌзюДѓШеЯњЪлРћШѓЪЧЖрЩйЃЎ
НтЃКЃЈ1ЃЉЩшвЛДЮКЏЪ§ЮЊy=kx+bЃЌНЋвЛДЮКЏЪ§жаЃЌЕУ
Ёрk=2 b=96
Ёрy=-2x+96
ОМьбщЃЌЦфЫќЕуЕФзјБъОљЪЪКЯвдЩЯНтЮіЪНЃЌ
ЁрЫљЧѓКЏЪ§НтЮіЪНЮЊy=-2x+96
ЃЈ2ЃЉЩшЧА20ЬьШеЯњЪлРћШѓЮЊWдЊ
W=(-2x+96)( ![]() x+25-20)
x+25-20)
=![]()
ЃЈ3ЃЉЁпЧА20ЬьШеЯњЪлРћШѓW
Ёп1ЁмxЁм20
ЁрЕБx=14ЪБЃЌWгазюДѓжЕ578(дЊ)
Кѓ20ЬьШеЯњЪлРћШѓЮЊSдЊЃЌ ![]()
ЕБ21ЁмxЁм40ЪБЃЌSЫцxЕФдіДѓЖјМѕаЁЁЃ
ЁрЕБx=21ЪБЃЌSгазюДѓжЕЮЊ540дЊЃЉ
Ёп578ЃО540ЃЌ
ЁрЕк14ЬьЪБЃЌЯњЪлРћШѓзюДѓЃЌЮЊ578дЊ
ЁАЕуОІЁБДЫЬтЗжБ№ПМВщСЫвЛДЮКЏЪ§ЁЂЖўДЮКЏЪ§ЕФгІгУЃЌНтЬтЕФЙиМќ ЪзЯШЖСЖЎЬтФПЃЌе§ШЗАбЮеЬтФПЕФЪ§СПЙиЯЕЃЌИљОнЪ§СПЙиЯЕЗжБ№СаГіКЏЪ§ЙиЯЕЪННтОіЮЪЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПEелЕўЃЌЪЙЕуBТфдкЕуBЁфДІЃЎЕБЁїCEBЁфЮЊжБНЧШ§НЧаЮЪБЃЌBEЕФГЄЮЊ ЃЎ 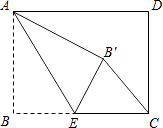
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
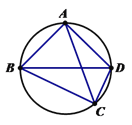
ЁОЬтФПЁПШчЭМЃЌЕуCЮЊЁїABDЭтНгдВЩЯЕФвЛЕуЃЈЕуCВЛдк![]() ЩЯЃЌЧвВЛгыЕуBЃЌDжиКЯЃЉЃЌЧвЁЯACB=ЁЯABD=45ЁуЃЌШєBC=8ЃЌCD=4ЃЌдђACЕФГЄЮЊЃЈ ЃЉ
ЩЯЃЌЧвВЛгыЕуBЃЌDжиКЯЃЉЃЌЧвЁЯACB=ЁЯABD=45ЁуЃЌШєBC=8ЃЌCD=4ЃЌдђACЕФГЄЮЊЃЈ ЃЉ
A. 8.5 B. ![]() C.
C. 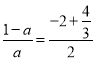 D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯђЖЋааЪЛ3kmЃЌМЧзї+3kmЃЌЯђЮїааЪЛ2kmМЧзїЃЈ ЃЉ
A.+2km
B.Љ2km
C.+3km
D.Љ3km
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гыxжсЃЌyжсЗжБ№НЛгкBЃЌCСНЕуЃЌХзЮяЯп
гыxжсЃЌyжсЗжБ№НЛгкBЃЌCСНЕуЃЌХзЮяЯп![]() ОЙ§BЃЌCСНЕуЃЌЕуAЪЧХзЮяЯпгыxжсЕФСэвЛИіНЛЕу.
ОЙ§BЃЌCСНЕуЃЌЕуAЪЧХзЮяЯпгыxжсЕФСэвЛИіНЛЕу.

ЃЈ1ЃЉЧѓГіЕуBКЭЕуCЕФзјБъ.
ЃЈ2ЃЉЧѓДЫХзЮяЯпЕФКЏЪ§НтЮіЪН.
ЃЈ3ЃЉдкХзЮяЯпxжсЩЯЗНДцдквЛЕуPЃЈВЛгыЕуCжиКЯЃЉЃЌЪЙ![]() ЃЌЧыЧѓГіЕуPЕФзјБъ.
ЃЌЧыЧѓГіЕуPЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСавђЪНЗжНтНсЙће§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.a2Љ9ЃНЃЈa+3ЃЉЃЈaЉ3ЃЉB.x2ЉxЃНxЃЈx2Љ1ЃЉ
C.x2+2x+4ЃНЃЈx+2ЃЉ2D.Љ4m3+12m2ЃНЉm2ЃЈ4mЉ12ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖЁАЪЋИшДѓЛсЁББШШќжаЃЌИїАрДњБэЖгЕУЗжШчЯТ(ЕЅЮЛЃКЗж)ЃК9ЃЌ7ЃЌ8ЃЌ7ЃЌ9ЃЌ7ЃЌ6ЃЌдђИїДњБэЖгЕУЗжЕФжаЮЛЪ§ЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌEЁЂFЗжБ№ЪЧABЁЂDCБпЩЯЕФЕуЃЌЧвAE=CFЃЌ 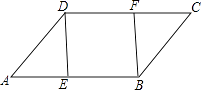
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁеЁїCBFЃЎ
ЃЈ2ЃЉШєЁЯDEB=90ЁуЃЌЧѓжЄЃКЫФБпаЮDEBFЪЧОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃН2ЃЈxЉ1ЃЉЃЈx+5ЃЉЕФЭМЯѓгыxжсЕФСНИіНЛЕужЎМфЕФОрРыЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com