
【题目】教材呈现:下图是华师版九年级上册数学教材第77页的部分内容.
猜想
如图,在![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 与
与![]() 的中点.根据画出的图形,可以猜想:
的中点.根据画出的图形,可以猜想:
![]() ,且
,且![]() .
.
对此,我们可以用演绎推理给出证明.

定理证明:请根据教材内容,结合图①,写出证明过程.
定理应用:
在矩形ABCD中,![]() ,AC为矩形ABCD的对角线,点E在边AB上,且
,AC为矩形ABCD的对角线,点E在边AB上,且![]() .
.
(1)如图②,点F在边CB上,连结EF.若![]() ,则EF与AC的关系为______________.
,则EF与AC的关系为______________.
(2)如图③,将线段AE绕点A旋转一定的角度![]() ,得到线段
,得到线段![]() ,连结
,连结![]() ,点H为
,点H为![]() 的中点,连结BH.设BH的长度为
的中点,连结BH.设BH的长度为![]() .若
.若![]() ,则
,则![]() 的取值范围为___________.
的取值范围为___________.

【答案】定理证明:见解析;定理应用:(1)EF∥AC,![]() ;(2)
;(2)![]() ≤m ≤
≤m ≤![]() .
.
【解析】
定理证明:利用![]() 及∠A=∠A可证得△ADE∽△ABC,再利用相似三角形的性质即可得证;
及∠A=∠A可证得△ADE∽△ABC,再利用相似三角形的性质即可得证;
定理应用:(1)利用![]() 及∠B=∠B可证得△BEF∽△BAC,进而再利用相似三角形的性质即可证得EF与AC的位置关系和数量关系;
及∠B=∠B可证得△BEF∽△BAC,进而再利用相似三角形的性质即可证得EF与AC的位置关系和数量关系;
(2)取AC中点F,连接BF、HF,易证得BF=![]() AC=
AC=![]() ,HF=
,HF=![]() AE'=
AE'=![]() ,再根据三角形三边关系即可得到m的取值范围.
,再根据三角形三边关系即可得到m的取值范围.
定理证明:
∵点D、E分别是AB与AC的中点,
∴![]() .
.
∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠ABC,![]() ,
,
∴DE∥BC,且![]() .
.
定理应用:
(1)解:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵∠B=∠B,
∴△BEF∽△BAC,
∴∠BEF=∠BAC,![]() ,
,
∴EF∥AC,![]() .
.
(2)解:如图,取AC中点F,连接BF、HF,

在矩形ABCD中,∠B=90°,BC=AD,
又∵![]() ,
,
∴BC=2,
∴在Rt△ABC中,![]()
∵∠B=90°,点F分别为AC的中点,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵点H、F分别为CE'、AC的中点,
∴![]() ,
,
∴当点H、F、B不在同一直线上时,![]() <m<
<m<![]() ,
,
当点H、F、B在同一直线上时,m=![]() 或m=
或m=![]() ,
,
综上所述,m的取值范围是![]() ≤m ≤
≤m ≤![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
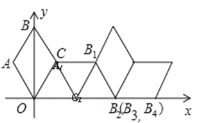
【题目】如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2016次,点B的落点依次为B1,B2,B3,…,则B2016的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
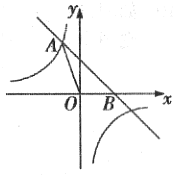
【题目】如图,直线y=﹣x+2与反比例函数y=![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
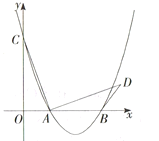
【题目】如图,在平面直角坐标系中,抛物线![]() (
(![]() 是常数,且
是常数,且![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() .连结
.连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() .当
.当![]() 最短时,
最短时,![]() 的值为_________ .
的值为_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数![]() 的图象位于
的图象位于![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折至其上方后,所得的是新函数
轴翻折至其上方后,所得的是新函数![]() 的图象.若该新函数图象与直线
的图象.若该新函数图象与直线![]() 有两个交点,则
有两个交点,则![]() 的取值范围为___________.
的取值范围为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数![]() 的图象位于
的图象位于![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折至其上方后,所得的是新函数
轴翻折至其上方后,所得的是新函数![]() 的图象.若该新函数图象与直线
的图象.若该新函数图象与直线![]() 有两个交点,则
有两个交点,则![]() 的取值范围为___________.
的取值范围为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
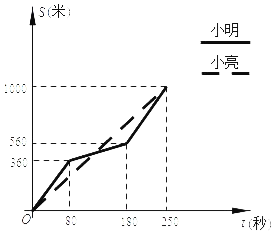
【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次男子1000米耐力测试中,小明和小亮同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示:
(1)当80≤t≤180时,求小明所跑的路程S(米)与所用的时间t(秒)之间的函数表达式;
(2)求他们第一次相遇的时间是起跑后的第几秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病,呼吸道疾病等,给人们造成困扰.为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图.

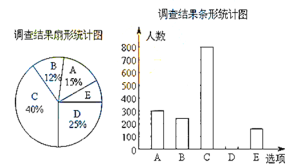
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有_________人;
(2)扇形统计图中,扇形![]() 的圆心角度数是__________;
的圆心角度数是__________;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com