
【题目】探究;
(![]() )如图,
)如图, ![]() 、
、![]() 为
为![]() 的边
的边![]() 、
、![]() 上的两定点,在
上的两定点,在![]() 上求作一点
上求作一点![]() ,使
,使![]() 的周长最短.(不写作法)
的周长最短.(不写作法)

(![]() )如图,矩形
)如图,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,求四边形
上的动点,求四边形![]() 周长的最小值.
周长的最小值.

(![]() )如图,正方形
)如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边中点,在边
边中点,在边![]() 、
、![]() 、
、![]() 上分别确定点
上分别确定点![]() 、
、![]() 、
、![]() .使得四边形
.使得四边形![]() 周长最小,并求出最小值.
周长最小,并求出最小值.

【答案】(1)作图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)
试题分析:(1)利用轴对称图形的性质,作点P关于BC的对称点P′,连接P′Q,交BC于点M,则M是所求的点;(2)如图,延长EB至E'使E' B=EB,延长FD至F'使F' D=FD,连接E' F'交BC、CD于M、N.此时四边形EFNM周长最小.根据勾股定理求得EF、E' F'的长,即可得四边形OMNP周长的最小值;(3)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .作
.作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .连
.连![]() 交
交![]() 于
于![]() ,即为周长最小.根据正方形的性质和轴对称的性质易得
,即为周长最小.根据正方形的性质和轴对称的性质易得![]() 、
、![]() 、
、![]() 为各边中点,所以四边形
为各边中点,所以四边形![]() 周长的最小值为
周长的最小值为![]() .
.
试题解析:
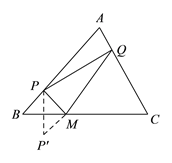
(![]() )如图,作点
)如图,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是所求的点.
是所求的点.
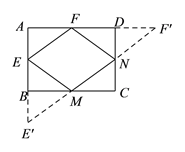
(![]() )如图,延长
)如图,延长![]() 至
至![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .此时四边形
.此时四边形![]() 周长最小.
周长最小.
周长![]()
![]()
![]() .
.
(![]() )如图,延长
)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .
.
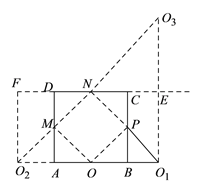
作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .
.
连![]() 交
交![]() 于
于![]() ,即为周长最小.
,即为周长最小.
易得![]() 、
、![]() 、
、![]() 为各边中点,周长为
为各边中点,周长为![]() .
.


科目:初中数学 来源: 题型:
【题目】某超市从一楼到二楼有一自动扶梯,如图是自动扶梯的侧面示意图,已知自动扶梯AB的坡度为1:2.4,AB的长度为13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处侧得C点的仰角为 42o,则二楼的层高BC约为(精确到0.1米,sin42o≈0.67,tan42o≈0.90)( )

A. 10.8米 B. 8.9米 C. 8.0米 D. 5.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,如果圆上有且只有两点到直线L的距离均为2,则半径r的取值范围是( )
A.r>1
B.r>2
C.2<r<2
D.1<r<5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小颖做掷骰子的游戏,规则如下:
① 游戏前,每人选一个数字;
② 每次同时掷两枚均匀骰子;
③ 如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.
(1)在下表中列出同时掷两枚均匀骰子所有可能出现的结果:
第2枚骰子掷得 第1枚 的点数 骰子掷得的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
1 | ||||||
2 | ||||||
3 | ||||||
4 | ||||||
5 | ||||||
6 |
(2)小明选的数字是5,小颖选的数字是6.如果你也加入游戏,你会选什么数字,使自
己获胜的概率比他们大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上周“双十二”瑞安某书店开展优惠购书活动:各类课外书活动时每本销售价格为y元,活动前每本销售价格为x(![]() )元,且y是x的一次函数,其中A类课外书与B类课外书活动前与活动时的价格如下表:
)元,且y是x的一次函数,其中A类课外书与B类课外书活动前与活动时的价格如下表:
图书类别 | 活动前的每本销售价格x(单位:元) | 活动时的每本销售价格y (单位:元) |
A类 | 28 | 21 |
B类 | 21 | 18 |
(1)求y关于x的一次函数表达式.
(2)当天小明购买了一本课外书,花费了24元,该课外书活动前的每本销售价格是多少元?
(3)在“双十二”优惠活动中,某学校花费不超过1900元,购买A、B两类课外书共100本,且B类课外书不超过70本,则可能有哪几种购书方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com