
【题目】如图,点P为x轴上一点,M为以P为圆心、PO为半径的圆上一点,过M作MN∥x轴交⊙P于另一点N,若M点的坐标为(-1,3),则点N的坐标为_____.
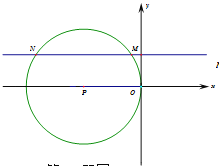
【答案】(-9,3)
【解析】
连接PM、PN、过点M作MA⊥x轴于点A,过点P作PB⊥MN于点B,设PO=r,则PM=PN=PO=r,由M坐标(﹣1,3)推出OA=1,MA=3,AP=(r-1),由勾股定理可得
![]() ,列关于r的一元二次方程,解方程得r=5,继而得P的坐标为(﹣5,0),根据平行线的性质可得N的纵坐标为3,根据矩形的判定和性质可得MB=AP=4,由垂径定理可得:NB=MB=4,继而推出N的横坐标为﹣9即可.
,列关于r的一元二次方程,解方程得r=5,继而得P的坐标为(﹣5,0),根据平行线的性质可得N的纵坐标为3,根据矩形的判定和性质可得MB=AP=4,由垂径定理可得:NB=MB=4,继而推出N的横坐标为﹣9即可.
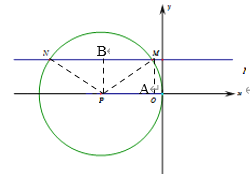
连接PM、PN、过点M作MA⊥x轴于点A,过点P作PB⊥MN于点B,设PO=r,则PM=PN=PO=r,
∵M坐标为(﹣1,3)
∴OA=1,MA=3,AP=PO﹣OA=r﹣1
在Rt△MPA中,由勾股定理可得
![]() ,即
,即![]() ,解得r=5,
,解得r=5,
∴圆心P的坐标为(﹣5,0)
∵MN∥x轴交⊙P于另一点N
∴N的纵坐标为3
∵PB⊥MN,MA⊥x轴,MN∥x轴
∴∠PBM=∠PAM=∠AMB=∠MBP=90°
∴四边形APBM是矩形,
∴MB=AP=5-1=4
由垂径定理可得:NB=MB=4
∴N的横坐标为:﹣5-4=﹣9
∴点N的坐标为(﹣9,3)
故答案为:(﹣9,3)


科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
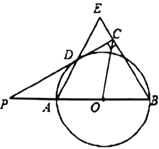
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
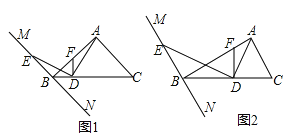
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
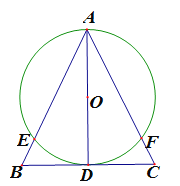
【题目】如图,△ABC中,AB=AC,AD⊥BC于D,以AD为直径的⊙O交AB于E,交AC于F.
(1)求证:BE=CF;
(2)若AE=4,BC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
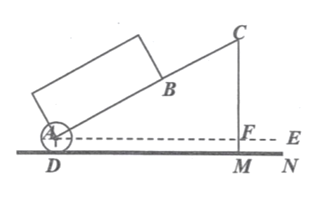
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长![]() ,拉杆最大伸长距离
,拉杆最大伸长距离![]() ,(点
,(点![]() 在同一条直线上),在箱体的底端装有一圆形滚轮
在同一条直线上),在箱体的底端装有一圆形滚轮![]() 与水平地面切于点
与水平地面切于点![]() 某一时刻,点
某一时刻,点![]() 距离水平面
距离水平面![]() ,点
,点![]() 距离水平面
距离水平面![]() .
.
(1)求圆形滚轮的半径![]() 的长;
的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点![]() 处且拉杆达到最大延伸距离时,点
处且拉杆达到最大延伸距离时,点![]() 距离水平地面
距离水平地面![]() ,求此时拉杆箱与水平面
,求此时拉杆箱与水平面![]() 所成角
所成角![]() 的大小(精确到
的大小(精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
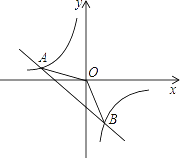
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com