
【题目】已知,如图1,抛物线![]() 过点
过点![]() 且对称轴为直线
且对称轴为直线![]() 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
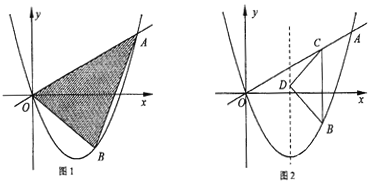
(1)求该抛物线的解析式:
(2)若△OAB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)如图2,过点B作直线BC∥y轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使△BCD是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)S![]() ,
, ![]() ;
;
(3)存在,点B为![]() 或
或![]()
【解析】试题分析:(1)根据抛物线![]() 过点
过点![]() 且对称轴为直线
且对称轴为直线![]() 即可求得结果;
即可求得结果;
(2)过点B作![]() 轴,交
轴,交![]() 于点
于点![]() ,则可得直线
,则可得直线![]() 为
为![]() ,则可设点
,则可设点![]() ,点
,点![]() 即可表示出BH,再根据三角形的面积公式即可表示出S关于m的函数关系式,根据二次函数的性质即可求得最大值;
即可表示出BH,再根据三角形的面积公式即可表示出S关于m的函数关系式,根据二次函数的性质即可求得最大值;
(3)设在抛物线的对称轴![]() 上存在点D满足题意,过点D作
上存在点D满足题意,过点D作![]() 于点Q,则由(2)有点
于点Q,则由(2)有点![]() ,点B
,点B![]() ,即可表示BC,由△BCD是以D为直角顶点的等腰直角三角形可得
,即可表示BC,由△BCD是以D为直角顶点的等腰直角三角形可得![]() ,则可得
,则可得![]() 且
且![]() ,再结合绝对值的性质分类讨论即可.
,再结合绝对值的性质分类讨论即可.
(1)由题知: 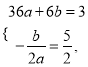 解之,得
解之,得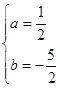
![]() 该抛物线的解析式为:
该抛物线的解析式为:![]()
(2)过点B作![]() 轴,交
轴,交![]() 于点
于点![]() 由题知直线
由题知直线![]() 为:
为:![]()
![]() 设点
设点![]() 点
点![]()
![]()
![]()
![]()
![]()
![]()
(3)设在抛物线的对称轴![]() 上存在点D满足题意,
上存在点D满足题意,
过点D作![]() 于点Q,则由(2)有点
于点Q,则由(2)有点![]() ,点B
,点B![]()
![]()
![]() 是以D为直角顶点的等腰直角三角形
是以D为直角顶点的等腰直角三角形
![]() 即是:
即是: ![]() 且
且![]()
若![]() 解之:
解之:![]() (舍去),
(舍去),![]()
![]() 时,
时, ![]()
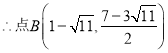
若![]() 解之:
解之:![]() (舍去)
(舍去)
当![]() 时,
时, ![]()
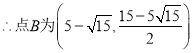
综上,满足条件的点B为![]() 或
或![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
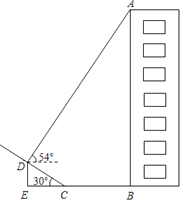
【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,求楼房AB的高度。(tan54°≈1.38,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月12号上映的《速度与激情7》在短短两周票房就突破了15.6亿,成为开年第一部现象级影片.该片已经打破了所有进口影片票房纪录.15.6亿用科学记数法表示是( )
A. 15.6×108B. 1.56×108C. 1.56×109D. 156×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com