
ΓΨΧβΡΩΓΩ–ΓάωΤο≥Β¥”ΦΉΒΊΒΫ““ΒΊΘ§–ΓΟςΤο≥Β¥”““ΒΊΒΫΦΉΒΊΘ§–ΓάωΒΡΥΌΕ»–Γ”Ύ–ΓΟςΒΡΥΌΕ»Θ§ΝΫ»ΥΆ§ ±≥ωΖΔΘ§―ΊΆ§“ΜΧθΙΪ¬Ζ‘»ΥΌ«ΑΫχ.ΆΦ÷–ΒΡ’έœΏ±μ ΨΝΫ»Υ÷°ΦδΒΡΨύάκ![]() ”κ–ΓάωΒΡ–– Μ ±Φδ
”κ–ΓάωΒΡ–– Μ ±Φδ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ.«κΡψΗυΨίΆΦœώΫχ––ΧΫΨΩΘΚ
÷°ΦδΒΡΚ· ΐΙΊœΒ.«κΡψΗυΨίΆΦœώΫχ––ΧΫΨΩΘΚ

Θ®1Θ©–ΓάωΒΡΥΌΕ» «______![]() Θ§–ΓΟςΒΡΥΌΕ» «_________
Θ§–ΓΟςΒΡΥΌΕ» «_________![]() ΘΜ
ΘΜ
Θ®2Θ©«σœΏΕΈ![]() Υυ±μ ΨΒΡy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΜ
Υυ±μ ΨΒΡy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©»τΝΫ»ΥœύΨύ![]() Θ§ ‘«σ–ΓάωΒΡ–– Μ ±ΦδΘΩ
Θ§ ‘«σ–ΓάωΒΡ–– Μ ±ΦδΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©10ΘΜ20ΘΜΘ®2Θ©![]()
![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]() –Γ ±Μρ2–Γ ±
–Γ ±Μρ2–Γ ±
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΚΆΚ· ΐΆΦœσ÷–ΒΡ ΐΨίΩ…“‘Ζ÷±π«σΒΟ–ΓάωΚΆ–ΓΟςΒΡΥΌΕ»ΘΜ
Θ®2Θ©ΗυΨίΘ®1Θ©÷–ΒΡΫαΙϊΚΆΆΦœσ÷–ΒΡ ΐΨίΩ…“‘«σΒΟΒψCΒΡΉχ±ξΘ§¥”ΕχΩ…“‘Ϋβ¥π±ΨΧβ
Θ®3Θ©ΗυΨίΧβ“βΖ÷«ιΩωΧ÷¬έΦ¥Ω…«σΫβ.
Θ®1Θ©¥”![]() Ω…“‘Ω¥≥ωΘΚΝΫ»Υ¥”œύΨύ30«ßΟΉΒΡΝΫΒΊœύ”ω”ΟΝΥ1Ηω–Γ ± ±ΦδΘ§
Ω…“‘Ω¥≥ωΘΚΝΫ»Υ¥”œύΨύ30«ßΟΉΒΡΝΫΒΊœύ”ω”ΟΝΥ1Ηω–Γ ± ±ΦδΘ§
‘ρ![]() «ßΟΉ/ ±Θ§–Γάω”ΟΝΥ3Ηω–Γ ±ΉΏΆξΝΥ30«ßΟΉΒΡ»Ϊ≥ΧΘ§
«ßΟΉ/ ±Θ§–Γάω”ΟΝΥ3Ηω–Γ ±ΉΏΆξΝΥ30«ßΟΉΒΡ»Ϊ≥ΧΘ§
Γύ![]() «ßΟΉ/ ±Θ§
«ßΟΉ/ ±Θ§
Γύ![]() «ßΟΉ/ ±ΘΜ
«ßΟΉ/ ±ΘΜ
Ι ¥πΑΗΈΣΘΚ10ΘΜ20ΘΜ
Θ®2Θ©CΒψΒΡ“β“ε «–ΓΟςΤο≥Β¥”““ΒΊΒΫΦΉΒΊ”ΟΝΥ![]() –Γ ±Θ§
–Γ ±Θ§
¥Υ ±–ΓάωΚΆ–ΓΟςΒΡΨύάκ «![]()
ΓύCΒψΉχ±ξ «![]() .
.
…η![]() Ε‘”ΠΒΡΚ· ΐ±μ¥ο ΫΈΣ
Ε‘”ΠΒΡΚ· ΐ±μ¥ο ΫΈΣ![]() Θ§
Θ§
‘ρΫΪΒψ![]() Θ§
Θ§![]() Ζ÷±π¥ζ»κ±μ¥ο ΫΒΟ
Ζ÷±π¥ζ»κ±μ¥ο ΫΒΟ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
ΓύBCΫβΈω ΫΈΣ![]() Θ§
Θ§![]()
Θ®3Θ©ΔΌΒ±ΝΫ»Υœύ”ω«ΑΘΚ![]() Θ®–Γ ±Θ©ΘΜ
Θ®–Γ ±Θ©ΘΜ
ΔΎΒ±ΝΫ»Υœύ”ωΚσΘΚ![]() Θ®–Γ ±Θ©.
Θ®–Γ ±Θ©.
¥πΘΚ–Γάω≥ωΖΔ![]() –Γ ±Μρ2–Γ ± ±Θ§ΝΫ»ΥœύΨύ20ΙΪάο.
–Γ ±Μρ2–Γ ± ±Θ§ΝΫ»ΥœύΨύ20ΙΪάο.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬ΟφΒΡ≤ΡΝœΘ§≤ΔΫβΨωΈ ΧβΘ°
Θ®1Θ©“―÷Σ‘ΎΓςABC÷–Θ§ΓœAΘΫ60ΓψΘ§ΆΦ1-ΆΦ3ΒΡΓςABCΒΡΡΎΫ«ΤΫΖ÷œΏΜρΆβΫ«ΤΫΖ÷œΏΫΜ”ΎΒψOΘ§«κ÷±Ϋ”«σ≥ωœ¬Ν–Ϋ«Ε»ΒΡΕ» ΐ.


»γΆΦ1Θ§ΓœOΘΫΓΓΓΓΓΓΓΓΓΓ; »γΆΦ2Θ§ΓœOΘΫΓΓΓΓΓΓΓΓΓΓ; »γΆΦ3Θ§ΓœOΘΫΓΓΓΓΓΓΓΓΓΓ;»γΆΦ4Θ§ΓœABCΘ§ΓœACBΒΡ»ΐΒ»Ζ÷œΏΫΜ”ΎΒψO1Θ§O2Θ§Ν§Ϋ”O1O2Θ§‘ρΓœBO2O1ΘΫΓΓΓΓΓΓΓΓΘ°
Θ®2Θ©»γΆΦ5Θ§ΒψO «ΓςABCΝΫΧθΡΎΫ«ΤΫΖ÷œΏΒΡΫΜΒψΘ§«σ÷ΛΘΚΓœOΘΫ90ΓψΘΪ![]() ΓœA.
ΓœA.
Θ®3Θ©»γΆΦ6Θ§ΓςABC÷–Θ§ΓœABCΒΡ»ΐΒ»Ζ÷œΏΖ÷±π”κΓœACBΒΡΤΫΖ÷œΏΫΜ”ΎΒψO1Θ§O2Θ§»τΓœ1ΘΫ115ΓψΘ§Γœ2ΘΫ135ΓψΘ§«σΓœAΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗω≤ΜΆΗΟςΒΡΩΎ¥ϋ÷–ΉΑ”–4ΗωΆξ»ΪœύΆ§ΒΡ–Γ«ρΘ§Ζ÷±π±ξ”– ΐΉ÷![]() Θ§Νμ“ΜΗωΩ…“‘Ή‘”…–ΐΉΣΒΡ‘≤≈ΧΘ§±ΜΖ÷≥…ΟφΜΐœύΒ»ΒΡ3Ηω…»–Έ«χ”ρΘ§Ζ÷±π±ξ”– ΐΉ÷
Θ§Νμ“ΜΗωΩ…“‘Ή‘”…–ΐΉΣΒΡ‘≤≈ΧΘ§±ΜΖ÷≥…ΟφΜΐœύΒ»ΒΡ3Ηω…»–Έ«χ”ρΘ§Ζ÷±π±ξ”– ΐΉ÷![]() Θ®»γΆΦΘ©.–Γ”±ΚΆ–ΓΝΝœκΆ®Ιΐ”ΈœΖά¥ΨωΕ®Υ≠¥ζ±μ―ß–Θ≤ΈΦ”Ηη”Ϋ±»»ϋΘ§”ΈœΖΙφ‘ρΈΣΘΚ“ΜΗω»ΥΩΎ¥ϋ÷–Οΰ≥ω“ΜΗω–Γ«ρΘ§Νμ“ΜΗω»ΥΉΣΕ·‘≤≈ΧΘ§»γΙϊΥυΟΰ«ρ…œΒΡ ΐΉ÷”κ‘≤≈Χ…œΉΣ≥ω ΐΉ÷÷°ΚΆ–Γ”Ύ4Θ§Ρ«Ο¥–Γ”±»ΞΘ§Ζώ‘ρ–ΓΝΝ»Ξ.
Θ®»γΆΦΘ©.–Γ”±ΚΆ–ΓΝΝœκΆ®Ιΐ”ΈœΖά¥ΨωΕ®Υ≠¥ζ±μ―ß–Θ≤ΈΦ”Ηη”Ϋ±»»ϋΘ§”ΈœΖΙφ‘ρΈΣΘΚ“ΜΗω»ΥΩΎ¥ϋ÷–Οΰ≥ω“ΜΗω–Γ«ρΘ§Νμ“ΜΗω»ΥΉΣΕ·‘≤≈ΧΘ§»γΙϊΥυΟΰ«ρ…œΒΡ ΐΉ÷”κ‘≤≈Χ…œΉΣ≥ω ΐΉ÷÷°ΚΆ–Γ”Ύ4Θ§Ρ«Ο¥–Γ”±»ΞΘ§Ζώ‘ρ–ΓΝΝ»Ξ.
Δ≈.”Ο ςΉ¥ΆΦΜρΝ–±μΖ®«σ≥ω–Γ”±≤ΈΦ”±»»ϋΒΡΗ≈¬ ΘΜ
ΔΤ.Ρψ»œΈΣΗΟ”ΈœΖΙΪΤΫ¬πΘΩ«κΥΒΟςάμ”…ΘΜ»τ≤ΜΙΪΤΫΘ§«κ–όΗΡΗΟ”ΈœΖΒΡΙφ‘ρΘ§ Ι”ΈœΖΙΪΤΫ.


≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–Γ¥œΚΆ–ΓΜέ―ΊΆΦl÷–ΒΡΖγΨΑ«χ”ΈάάΘ§‘ΦΚΟ‘ΎΖ…ΤΌΦϊΟφ.–Γ¥œΦί ΜΒγΕ·Τϊ≥Β¥”±ωΙί≥ωΖΔΘ§–ΓΜέ“≤”ΎΆ§“Μ ±ΦδΤοΒγΕ·Ή‘––≥Β¥”ΥΰΝ÷≥ωΖΔ.ΆΦ2÷–ΒΡΆΦœώΖ÷±π±μ ΨΝΫ»Υάκ±ωΙίΒΡ¬Ζ≥Χ![]() ”κ ±Φδ
”κ ±Φδ![]() ΒΡΚ· ΐΙΊœΒΘ§ ‘ΫαΚœΆΦ÷––≈œΔΜΊ¥πΘΚ
ΒΡΚ· ΐΙΊœΒΘ§ ‘ΫαΚœΆΦ÷––≈œΔΜΊ¥πΘΚ

Θ®1Θ©Ζ…ΤΌ”κ±ωΙίœύΨύ__________![]() Θ§–Γ¥œ≥ωΖΔ
Θ§–Γ¥œ≥ωΖΔ![]() ±”κ±ωΙίΒΡΨύάκ
±”κ±ωΙίΒΡΨύάκ![]() _________
_________![]() ΘΜ
ΘΜ
Θ®2Θ©»τ–Γ¥œ≥ωΖΔ![]() ΚσΘ§ΥΌΕ»±δΈΣ–ΓΜέΒΡ2±ΕΘ§‘ρ–Γ¥œΉΖ…œ–ΓΜέ ±Θ§ΥϊΟ« «Ζώ“―Ψ≠ΙΐΝΥ≤ίΒιΘΩ
ΚσΘ§ΥΌΕ»±δΈΣ–ΓΜέΒΡ2±ΕΘ§‘ρ–Γ¥œΉΖ…œ–ΓΜέ ±Θ§ΥϊΟ« «Ζώ“―Ψ≠ΙΐΝΥ≤ίΒιΘΩ
Θ®3Θ©Β±≥ωΖΔΕύ≥Λ ±Φδ ±Θ§ΝΫ»ΥœύΨύ![]() ΘΩ
ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ“ΜΉι ΐΨίx1Θ§x2Θ§x3Θ§x4Θ§x5ΒΡΤΫΨυ ΐ «2Θ§ΖΫ≤ν «![]() Θ§Ρ«Ο¥Νμ“ΜΉι ΐΨί3x1©¹2Θ§3x2©¹2Θ§3x3©¹2Θ§3x4©¹2Θ§3x5©¹2ΒΡΤΫΨυ ΐΚΆΖΫ≤νΖ÷±π «Θ®ΓΓΓΓΘ©
Θ§Ρ«Ο¥Νμ“ΜΉι ΐΨί3x1©¹2Θ§3x2©¹2Θ§3x3©¹2Θ§3x4©¹2Θ§3x5©¹2ΒΡΤΫΨυ ΐΚΆΖΫ≤νΖ÷±π «Θ®ΓΓΓΓΘ©
A. 2Θ§![]() B. 2Θ§1 C. 4Θ§
B. 2Θ§1 C. 4Θ§![]() D. 4Θ§3
D. 4Θ§3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΐ―ß–Υ»Λ–ΓΉιΈΣΝΥΫβΈ“–Θ≥θ»ΐΡξΦΕ1800Οϊ―ß…ζΒΡ…μΧεΫΓΩΒ«ιΩωΘ§¥”≥θ»ΐΥφΜζ≥ι»ΓΝΥ»τΗ…Οϊ―ß…ζΘ§ΫΪΥϊΟ«Α¥Χε÷ΊΘ®ΨυΈΣ’ϊ ΐΘ§ΒΞΈΜΘΚkgΘ©Ζ÷≥…ΈεΉιΘ®AΘΚ39.5ΓΪ46.5ΘΜBΘΚ46.5ΓΪ53.5ΘΜCΘΚ53.5ΓΪ60.5ΘΜDΘΚ60.5ΓΪ67.5ΘΜEΘΚ67.5ΓΪ74.5Θ©Θ§≤Δ“άΨίΆ≥ΦΤ ΐΨίΜφ÷ΤΝΥ»γœ¬ΝΫΖυ…–≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°

≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ§≤ΔΙάΦΤΈ“–Θ≥θ»ΐΡξΦΕΧε÷ΊΫι”Ύ47kg÷Ν53kgΒΡ―ß…ζ¥σ‘Φ”–Εύ…ΌΟϊΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΝβ–ΈABCD÷–Θ§FΈΣ±ΏBCΒΡ÷–ΒψΘ§DF”κΕ‘Ϋ«œΏACΫΜ”ΎΒψMΘ§ΙΐMΉςMEΓΆCD”ΎΒψEΘ§Γœ1=Γœ2Θ°
Θ®1Θ©»τCE=1Θ§«σBCΒΡ≥ΛΘΜ
Θ®2Θ©«σ÷ΛΘΚAM=DF+MEΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪΝΫΗω»ΪΒ»ΒΡ÷±Ϋ«»ΐΫ«–ΈΓςABDΓΔΓςACEΤ¥‘Ύ“ΜΤπΘ®ΆΦΘ®1Θ©Θ©Θ°ΝνΓςABD≤ΜΕ·Θ§
Θ®1Θ©»τΫΪΓςACE»ΤΒψAΡφ ±’κ–ΐΉΣΘ§Ν§Ϋ”DEΘ§M «DEΒΡ÷–ΒψΘ§Ν§Ϋ”MBΓΔMCΘ®ΆΦΘ®2Θ©Θ©Θ§÷ΛΟςΘΚMB=MCΘ°
Θ®2Θ©»τΫΪΆΦΘ®1Θ©÷–ΒΡCEœρ…œΤΫ“ΤΘ§ΓœCAE≤Μ±δΘ§Ν§Ϋ”DEΘ§M «DEΒΡ÷–ΒψΘ§Ν§Ϋ”MBΓΔMCΘ®ΆΦΘ®3Θ©Θ©Θ§≈–ΕœMBΓΔMCΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
Θ®3Θ©‘ΎΘ®2Θ©÷–Θ§»τΓœCAEΒΡ¥σ–ΓΗΡ±δΘ®ΆΦΘ®4Θ©Θ©Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§‘ρΘ®2Θ©÷–ΒΡMBΓΔMCΒΡ ΐΝΩΙΊœΒΜΙ≥…ΝΔ¬πΘΩΥΒΟςάμ”….

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§ΙΐΕΞΒψ
Θ§ΙΐΕΞΒψ![]() Ής…δœΏ
Ής…δœΏ![]() .
.
Θ®1Θ©Β±…δœΏ![]() ‘Ύ
‘Ύ![]() Άβ≤Ω ±Θ§»γΆΦΔΌΘ§Βψ
Άβ≤Ω ±Θ§»γΆΦΔΌΘ§Βψ![]() ‘Ύ…δœΏ
‘Ύ…δœΏ![]() …œΘ§Ν§Ϋα
…œΘ§Ν§Ϋα![]() ΓΔ
ΓΔ![]() Θ§“―÷Σ
Θ§“―÷Σ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ®
Θ®![]() Θ©.
Θ©.
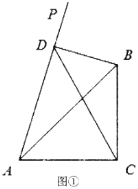
ΔΌ ‘÷ΛΟς![]() «÷±Ϋ«»ΐΫ«–ΈΘΜ
«÷±Ϋ«»ΐΫ«–ΈΘΜ
ΔΎ«σœΏΕΈ![]() ΒΡ≥Λ.Θ®”ΟΚ§
ΒΡ≥Λ.Θ®”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
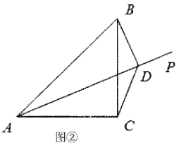
Θ®2Θ©Β±…δœΏ![]() ‘Ύ
‘Ύ![]() ΡΎ≤Ω ±Θ§»γΆΦΔΎΘ§ΙΐΒψ
ΡΎ≤Ω ±Θ§»γΆΦΔΎΘ§ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋα
Θ§Ν§Ϋα![]() Θ§«κ–¥≥ωœΏΕΈ
Θ§«κ–¥≥ωœΏΕΈ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”….
ΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com