
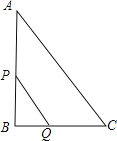
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌACЃН10cmЃЌBCЃН6cmЃЌЯжгаСНИіЖЏЕуPЁЂQЗжБ№ДгЕуAКЭЕуBЭЌЪБГіЗЂЃЌЦфжаЕуPвд2cm/sЕФЫйЖШЃЌбиABЯђжеЕуBвЦЖЏЃЛЕуQвд1cm/sЕФЫйЖШбиBCЯђжеЕуCвЦЖЏЃЌЦфжавЛЕуЕНжеЕуЃЌСэвЛЕувВЫцжЎЭЃжЙЃЎСЌНгPQЃЎЩшЖЏЕудЫЖЏЪБМфЮЊxУыЃЎ
ЃЈ1ЃЉгУКЌxЕФДњЪ§ЪНБэЪОBQЁЂPBЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБxЮЊКЮжЕЪБЃЌЁїPBQЮЊЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉЪЧЗёДцдкxЕФжЕЃЌЪЙЕУЫФБпаЮAPQCЕФУцЛ§ЕШгк20cm2ЃПШєДцдкЃЌЧыЧѓГіДЫЪБxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉBQЃНxЃЌPBЃН8Љ2xЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉДцдкЃЌxЃН2.
ЃЛЃЈ3ЃЉДцдкЃЌxЃН2.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнТЗГЬ=ЫйЖШЁСЪБМфЧѓГіBQЃЌAPЃЌдйИљОнPB=AB-APМДПЩ.
ЃЈ2ЃЉИљОнЬтвтЃЌЕБЁїPBQЮЊЕШбќШ§НЧаЮЪБЃЌBQ=PBЃЌНЈСЂвЛИіЙигкxЕФЗНГЬЃЌНтЗНГЬМДПЩ.
ЃЈ3ЃЉгУКЌxЕФДњЪ§ЪНБэЪОГіЫФБпаЮAPQCЕФУцЛ§ЃЌРћгУЫФБпаЮAPQCЕФУцЛ§ЮЊ20НЈСЂвЛИіЙигкxЗНГЬЃЌНтЗНГЬМДПЩ.ШєгаНтЃЌдђДцдкЃЌШєЮоНтдђВЛДцдк.
НтЃКЃЈ1ЃЉЁпЁЯBЃН90ЁуЃЌACЃН10ЃЌBCЃН6ЃЌ
ЁрABЃН8ЃЎ
ЁрBQЃНxЃЌPB=AB-APЃН8Љ2xЃЛ
ЃЈ2ЃЉгЩЬтвтЃЌЕУ
8Љ2xЃНxЃЌ
ЁрxЃН![]() ЃЎ
ЃЎ
ЁрЕБxЃН![]() ЪБЃЌЁїPBQЮЊЕШбќШ§НЧаЮЃЛ
ЪБЃЌЁїPBQЮЊЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉМйЩшДцдкxЕФжЕЃЌЪЙЕУЫФБпаЮAPQCЕФУцЛ§ЕШгк20cm2ЃЌ
дђ![]()
НтЕУx1ЃНx2ЃН2ЃЎ
МйЩшГЩСЂЃЌЫљвдЕБxЃН2ЪБЃЌЫФБпаЮAPQCУцЛ§ЕФУцЛ§ЕШгк20cm2ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃзМБИдкаЃдАФкаоНЈвЛИіОиаЮЕФТЬЛЏДјЃЌОиаЮЕФУцЛ§ЮЊЖЈжЕЃЌЫќЕФвЛБпГЄ![]() гыСэвЛБпГЄ
гыСэвЛБпГЄ![]() жЎМфЕФКЏЪ§ЭМЯёШчЭМ.
жЎМфЕФКЏЪ§ЭМЯёШчЭМ.

ЃЈ1ЃЉИУТЬЛЏДјЕФУцЛ§ЪЧЖрЩйЃПаДГі![]() гы
гы![]() ЕФКЏЪ§НтЮіЪН.
ЕФКЏЪ§НтЮіЪН.
ЃЈ2ЃЉЭъГЩЯТБэЃЌВЂЛиД№ЮЪЬтЃКШчЙћИУТЬЛЏДјЕФГЄ![]() ВЛЕУГЌЙ§
ВЛЕУГЌЙ§![]() ЃЌФЧУД
ЃЌФЧУД![]() гІПижЦдкЪВУДЗЖЮЇЃП
гІПижЦдкЪВУДЗЖЮЇЃП
| 10 | 20 | 30 | 40 |
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
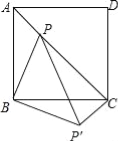
ЁОЬтФПЁПШчЭМЃЌPЮЊе§ЗНаЮABCDФквЛЕуЃЌЧвBP=2ЃЌPC=3ЃЌЁЯAPB=135ЁуЃЌНЋЁїAPBШЦЕуBЫГЪБеыа§зЊ90ЁуЕУЕНЁїCPЁфBЃЌСЌНгPPЁфЃЌдђAP= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌжБЯпCDгывдЯпЖЮOBЮЊжБОЖЕФАыЁбAЯрЧагкЕуCЃЌСЌНгOCЁЂBCЃЌзїODЁЭCDЃЌДЙзуЮЊDЃЌOBЃН10ЃЌ
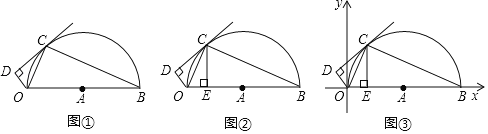
ЃЈ1ЃЉЧѓжЄЃКЁЯOCDЃНЁЯOBCЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌзїCEЁЭOBгкЕуEЃЌШєCEЃНAEЃЌЧѓЯпЖЮODЕФГЄЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌвдOЕуЮЊдЕуНЈСЂЦНУцжБНЧзјБъЯЕЧѓЁїDOBЭтНгдВЕФдВаФзјБъЃЎ
вдЯТЪЧгХгХКЭРжРжСНЮЛЭЌбЇЖдЕкЃЈ3ЃЉаЁЬтЕФЬжТл
гХгХЃКетЬтКмМђЕЅТяЃЌЮвжЛвЊЧѓГіетИіШ§НЧаЮШЮвтСНЬѕБпЕФжаДЙЯпНтЮіЪНЃЌШЛКѓЧѓНЛЕузјБъОЭааСЫЃЎРжРжЃКЮвЛЙгаЦфЫћЕФКУЗНЗЈЃЎ
ШчЙћФуЪЧРжРжЃЌФуЛсдѕУДзіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() гы
гы![]() ЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЧв
ЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌСЌНгDCЃЌЕуMЁЂPЁЂNЗжБ№ЮЊDEЁЂDCЁЂBCЕФжаЕу
ЃЌСЌНгDCЃЌЕуMЁЂPЁЂNЗжБ№ЮЊDEЁЂDCЁЂBCЕФжаЕу
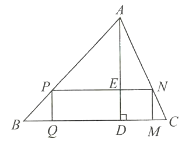
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуDЁЂEЗжБ№дкБпABЁЂACЩЯЃЌЯпЖЮPMгыPNЕФЪ§СПЙиЯЕЪЧ______ЃЌЮЛжУЙиЯЕЪЧ______ЃЛ
ЃЈ2ЃЉАбЕШбќ![]() ШЦЕуAа§зЊЕНШчЭМ2ЕФЮЛжУЃЌСЌНгMNЃЌХаЖЯ
ШЦЕуAа§зЊЕНШчЭМ2ЕФЮЛжУЃЌСЌНгMNЃЌХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉАбЕШбќ![]() ШЦЕуAдкЦНУцФкШЮвта§зЊЃЌ
ШЦЕуAдкЦНУцФкШЮвта§зЊЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() ЕФУцЛ§SЕФБфЛЏЗЖЮЇЃЎ
ЕФУцЛ§SЕФБфЛЏЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() ЪЧвЛПщШёНЧШ§НЧаЮгрСЯЃЌБп
ЪЧвЛПщШёНЧШ§НЧаЮгрСЯЃЌБп![]() КСУзЃЌИп
КСУзЃЌИп![]() КСУзЃЌвЊАбЫќМгЙЄГЩвЛИіОиаЮСуМўЃЌЪЙОиаЮЕФвЛБпдк
КСУзЃЌвЊАбЫќМгЙЄГЩвЛИіОиаЮСуМўЃЌЪЙОиаЮЕФвЛБпдк![]() ЩЯЃЌЦфгрСНИіЖЅЕуЗжБ№дк
ЩЯЃЌЦфгрСНИіЖЅЕуЗжБ№дк![]() ЃЌ
ЃЌ![]() ЩЯЃЌЩшИУОиаЮЕФГЄ
ЩЯЃЌЩшИУОиаЮЕФГЄ![]() КСУзЃЌПэ
КСУзЃЌПэ![]() КСУз.
КСУз.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() гы
гы![]() ЗжБ№ШЁЪВУДжЕЪБЃЌОиаЮ
ЗжБ№ШЁЪВУДжЕЪБЃЌОиаЮ![]() ЕФУцЛ§зюДѓЃПзюДѓУцЛ§ЪЧЖрЩйЃП
ЕФУцЛ§зюДѓЃПзюДѓУцЛ§ЪЧЖрЩйЃП
ЃЈ3ЃЉЕБОиаЮ![]() ЕФУцЛ§зюДѓЪБЃЌЫќЕФГЄКЭПэЪЧЙигк
ЕФУцЛ§зюДѓЪБЃЌЫќЕФГЄКЭПэЪЧЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЕФСНИіИљЃЌЖј
ЕФСНИіИљЃЌЖј![]() ЃЌ
ЃЌ![]() ЕФжЕгжЧЁКУЗжБ№ЪЧ
ЕФжЕгжЧЁКУЗжБ№ЪЧ![]() ЃЌ10ЃЌ12ЃЌ13ЃЌ
ЃЌ10ЃЌ12ЃЌ13ЃЌ![]() ет5ИіЪ§ОнЕФжкЪ§гыЦНОљЪ§ЃЌЪдЧѓ
ет5ИіЪ§ОнЕФжкЪ§гыЦНОљЪ§ЃЌЪдЧѓ![]() гы
гы![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЁЂ
ЁЂ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ![]() дк
дк![]() ЩЯЃЌжБЯп
ЩЯЃЌжБЯп![]() ЁЂ
ЁЂ![]() НЛгк
НЛгк![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() НЛгк
НЛгк![]() ЃЌЕБ
ЃЌЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЃЈВЛгы
ЃЈВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЩЯдЫЖЏЪБЃЌЯТСаЫФИіНсТлЃКЂй
жиКЯЃЉЩЯдЫЖЏЪБЃЌЯТСаЫФИіНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЁЂ
ЁЂ![]() ЫљМаЕФШёНЧЮЊ
ЫљМаЕФШёНЧЮЊ![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂмШє
ЃЛЂмШє![]() ЦНЗж
ЦНЗж![]() ЃЌдђе§ЗНаЮ
ЃЌдђе§ЗНаЮ![]() ЕФУцЛ§ЮЊ4ЃЌЦфжаНсТле§ШЗЕФЪЧ__ЃЈЬюађКХЃЉ
ЕФУцЛ§ЮЊ4ЃЌЦфжаНсТле§ШЗЕФЪЧ__ЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
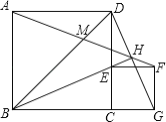
ЁОЬтФПЁПШчЭМе§ЗНаЮABCDЃЌEЁЂFЗжБ№ЮЊBCЁЂCDБпЩЯвЛЕуЃЎ
ЃЈ1ЃЉШєЁЯEAFЃН45ЁуЃЌЧѓжЄЃКEFЃНBE+DFЃЛ
ЃЈ2ЃЉШєИУе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌШчЙћЁїCEFЕФжмГЄЮЊ2ЃЎЧѓЁЯEAFЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
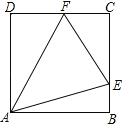
ЁОЬтФПЁПШчЭМЃЌвЛИіЖўДЮКЏЪ§ЕФЭМЯёОЙ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЃЌЕу
Ш§ЕуЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌЧв
жсЕФе§АыжсЩЯЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉздБфСП![]() дкЪВУДЗЖЮЇФкЪБЃЌ
дкЪВУДЗЖЮЇФкЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃПКЮЪБЃЌ
ЕФдіДѓЖјдіДѓЃПКЮЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁ
ЕФдіДѓЖјМѕаЁ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com