
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连结O1A、O1B、O2A、O2B和AB。
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)在(2)中,当重叠部分图形的周长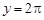 时,则线段O2A所在的直线与⊙O1有何位置关系?请说明理由.除此之外,它们是否还有其它的位置关系?如果有,请直接写出其它位置关系时的x的取值范围.
时,则线段O2A所在的直线与⊙O1有何位置关系?请说明理由.除此之外,它们是否还有其它的位置关系?如果有,请直接写出其它位置关系时的x的取值范围.
(1)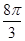 (2)
(2)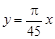 (0≤x≤180) (3)O2A与⊙O1相切;当0≤x≤90和0≤x≤180时,线段O2A所在的直线与⊙O1相交
(0≤x≤180) (3)O2A与⊙O1相切;当0≤x≤90和0≤x≤180时,线段O2A所在的直线与⊙O1相交
【解析】
试题分析:(1)解法一、依对称性得,∠AO2B=∠AO1B=120°,
∴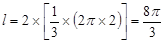
解法二、∵O1A=O1B=O2A=O2B
∴AO1BO2是菱形 ∴∠AO2B=∠AO1B=120°
∴l=2×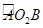 =
=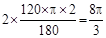
(2)∵由(1)知,菱形AO1BO2中∠AO2B=∠AO1B=x度,
∴重叠图形的周长 , 即
, 即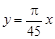 (0≤x≤180)
(0≤x≤180)
(3) 当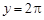 时,线段O2A所在的直线与⊙O1相切!
时,线段O2A所在的直线与⊙O1相切!
理由如下:∵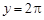 ,由(2)可知:
,由(2)可知: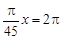 , 解之x=90度
, 解之x=90度
∴AO1B=90°,因此菱形AO1BO2是正方形,∴O1AO2=90°,即O2A⊥O1A,
而O1A是⊙O1的半径,且A为半径之外端;∴O2A与⊙O1相切。
还有如下位置关系:当0≤x≤90和0≤x≤180时,线段O2A所在的直线与⊙O1相交
考点:直线与圆的位置关系
点评:本题主要考查直线与圆的位置关系,掌握判定直线与圆的位置关系是解本题的关键,会求函数的解析式,本题难度比较大


科目:初中数学 来源: 题型:
 25、如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.
25、如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.查看答案和解析>>
科目:初中数学 来源: 题型:
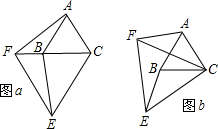 F和BE
F和BE查看答案和解析>>
科目:初中数学 来源: 题型:
| CD1 |
| DD1 |
| 4 |
| 3 |
| 4 |
| 3 |
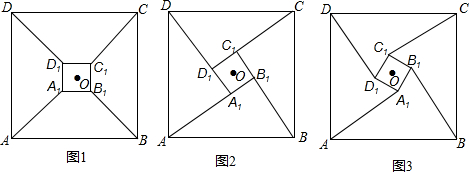
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com