
【题目】锐角![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高线,
边上的高线,![]() ,两动点
,两动点![]() 分别在边
分别在边![]() 上滑动,且
上滑动,且![]() ,以
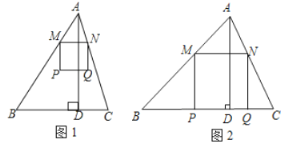
,以![]() 为边向下作正方形
为边向下作正方形![]() (如图1),设其边长为
(如图1),设其边长为![]() .
.
(1)当![]() 恰好落在边
恰好落在边![]() 上(如图2)时,求
上(如图2)时,求![]() ;
;
(2)正方形![]() 与
与![]() 公共部分的面积为
公共部分的面积为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或4.
或4.
【解析】
(1)根据已知条件,求出AD的值,再由△AMN∽△ABC,确定比例关系求出x的值即可;
(2)当正方形![]() 与
与![]() 公共部分的面积为
公共部分的面积为![]() 时,可分两种情况,一是当
时,可分两种情况,一是当![]() 在△ABC的内部,二是当
在△ABC的内部,二是当![]() 在△ABC的外部,当当
在△ABC的外部,当当![]() 在△ABC的外部时,根据相似,表达出重叠部分面积,再列出方程,解出x的值即可.
在△ABC的外部时,根据相似,表达出重叠部分面积,再列出方程,解出x的值即可.
解:(1)∵![]() ,
,![]() 为
为![]() 边上的高线,
边上的高线,![]() ,
,
∴![]()
∴AD=4,
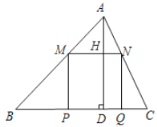
设AD交MN于点H,
∵MN∥BC,
∴△AMN∽△ABC,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴当![]() 恰好落在边
恰好落在边![]() 上时,
上时,![]()
(2)①当![]() 在△ABC的内部时,正方形
在△ABC的内部时,正方形![]() 与
与![]() 公共部分的面积即为正方形
公共部分的面积即为正方形![]() 的面积,
的面积,
∴![]() ,解得
,解得![]()
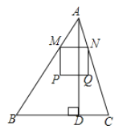
②当![]() 在△ABC的外部时,如下图所示,PM交BC于点E,QN交BC于点F,AD交MN于点H,
在△ABC的外部时,如下图所示,PM交BC于点E,QN交BC于点F,AD交MN于点H,
设HD=a,则AH=4-a,
由![]() 得
得![]() ,解得
,解得![]()
∴矩形MEFN的面积为![]()
即![]()
解得![]() (舍去),
(舍去),
综上:正方形![]() 与
与![]() 公共部分的面积为
公共部分的面积为![]() 时,
时,![]() 或4.
或4.


科目:初中数学 来源: 题型:
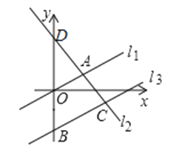
【题目】如图,在平面直角坐标系中,直线![]() 与直线
与直线![]() ,交点
,交点![]() 的横坐标为
的横坐标为![]() ,将直线
,将直线![]() ,沿
,沿![]() 轴向下平移
轴向下平移![]() 个单位长度,得到直线
个单位长度,得到直线![]() ,直线
,直线![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() ,交于点
,交于点![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,直线
,直线![]() ;与
;与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
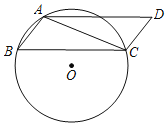
【题目】操作、证明:如图,在平行四边形ABCD中,连接AC,以点C为圆心BC为半径画弧,交△ABC的外接圆O于点E,连接AE、CE.
(1)求证:AD=CE,∠D=∠E.
(2)连接CO,求证:CO平分∠BCE.
(3)判断:“一组对边相等且一组对角相等的四边形是平行四边形”是 命题(填“真”或“假”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的
轴的![]() 个交点坐标为
个交点坐标为![]() ,
,![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
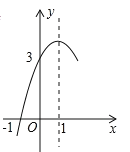
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
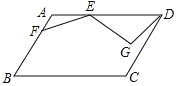
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E在AD上,且AE=4,点
,点E在AD上,且AE=4,点![]() 是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为____________________.
是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
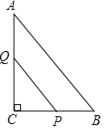
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在边BC、AC上,PQ∥AB,把△PCQ绕点P旋转得到△PDE(点C、Q分别与点D、E对应),点D落在线段PQ上,若AD平分∠BAC,则CP的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射击比赛,每人射击五次,命中的环数如下表:
次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲命中的环数(环) | 6 | 7 | 8 | 6 | 8 |
乙命中的环数(环) | 5 | 10 | 7 | 6 | 7 |
根据以上数据,下列说法正确的是( )
A.甲的平均成绩大于乙B.甲、乙成绩的中位数不同
C.甲、乙成绩的众数相同D.甲的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
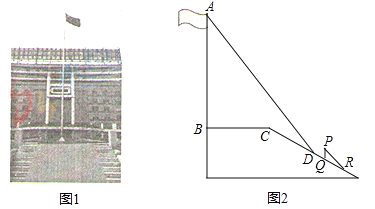
【题目】(2016山东省烟台市)某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com