
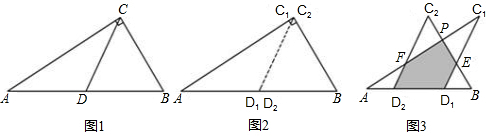
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图2所示).将纸片△AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一直线上),当点D1与点B重合时,停止平移.在平移的过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P.
1.当△AC1D1平移到如图3所示位置时,猜想D1E与D2F的数量关系,并说明理由
2.设平移距离D2D1为x,△AC1D1和△BC2D2重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
3.对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的![]() ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.

图1 图2 图3
1.. ……………………1分
∵,∴
.∠C2=∠BED1
又∵∠ACB=90°,CD是斜边上的中线,
∴, DC=DA=DB,即
∴,∠C2=∠B ∴
, ∠BED1=∠B ……………2分
∴,.
.
又∵,∴
.∴
……………………3分
2.∵在Rt△ABC中,AC=8,BC=6,所以由勾股定理,得AB=10.
即
又∵,∴
.∴
在中,
到
的距离就是△ABC的AB边上的高,为
.
设的
边上的高为h,由探究,得
,∴
.
∴.
.……………………6分
又∵,∴
.
又∵,
.
∴,
而
∴. ……………8分
3.存在. ………………9分
当时,即
整理,得.解得,
.………………11分
即当或
时,重叠部分的面积等于原△ABC面积的
.……12分
解析:(1)根据题意,易得∠C1=∠AFD2;进而可得C1D1=C2D2=BD2=AD1,又因为AD1=BD2,可得答案;
(2)因为在Rt△ABC中,AC=8,BC=6,所以由勾股定理,得AB=10;又因为C2D1=x,所以D1E=BD1=D2F=AD2=5-x,由图形可得阴影部分面积的组成,分别用x表示出其面积可得答案.
(3)存在,解关于x的运用二次方程求得


科目:初中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》常考题集(24):34.4 二次函数的应用(解析版) 题型:解答题
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(41):2.4 二次函数的应用(解析版) 题型:解答题
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年广东省汕头市龙湖区中考数学模拟试卷(解析版) 题型:解答题
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com