一枚均匀的正方体骰子,六个面分别标有数字1,2,3,4,5,6.如果用小刚抛掷正方体骰子朝上的数字m和小强抛掷正方体骰子朝上的数字n来确定点P(m,n),那么他们各抛掷一次所确定的点P落在直线y=x+2图象上的概率是多少?
【答案】
分析:首先根据题意列出表格,然后根据表格求得所有等可能的情况与点(1,3)、(2,4)、(3、5)、(4,6)在直线y=x+2的图象上,然后利用概率公式求解即可求得答案.
解答:解:列表表示如下:…(6分)
| nm | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
由表格易知,共有36种可能情况,点(1,3)、(2,4)、(3、5)、(4,6)在直线y=x+2的图象上,
因此他们各抛掷一次所确定的点P落在直线y=x+2图象上的概率是:
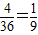
.…(12分)
点评:此题考查了列表法与树状图法求概率的知识以及一次函数图象上点的坐标特征.此题比较简单,注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

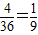 .…(12分)
.…(12分)

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案