
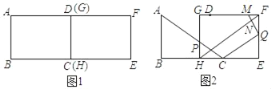
【题目】把两个全等的矩形ABCD和EFGH如图1摆放(点D和点G重合,点C和点H重合),点A、D(G)在同一条直线上,AB=6cm,BC=8cm.如图2,△ABC从图1位置出发,沿BC方向匀速运动,速度为1cm/s,AC与GH交于点P;同时,点Q从点E出发,沿EF方向匀速运动,速度为1cm/s.点Q停止运动时,△ABC也停止运动.设运动时间为t(s)(0<t<6).
(1)当t为何值时,CQ∥FH;
(2)过点Q作QM⊥FH于点N,交GF于点M,设五边形GBCQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在(2)的条件下,是否存在某一时刻,使点M在线段PC的中垂线上?若存在,请求出t的值;若不存在,请说明理由.
【答案】(1)t=![]() 时,CQ∥FH;(2)
时,CQ∥FH;(2)![]() (3)存在某一时刻,使点M在线段PC的中垂线上,t的值为
(3)存在某一时刻,使点M在线段PC的中垂线上,t的值为![]() s.
s.
【解析】
(1)由矩形的性质得出BC=EH=GF=8cm,AB=EF=6cm,∠1B=∠E=∠EFG=90°,由勾股定理得出AC=FH=10(cm),由平行线得出△CEQ∽△HEF,根据相似三角形对应边成比例即可得出答案;
(2)证明△FMQ∽△EFH,得出![]() ,求出MF=
,求出MF=![]() (6﹣t),当0<t<6时,五边形GBCQM的面积为y=梯形GBEF的面积﹣△CEQ的面积﹣△MFQ的面积,代入面积公式进行计算即可;
(6﹣t),当0<t<6时,五边形GBCQM的面积为y=梯形GBEF的面积﹣△CEQ的面积﹣△MFQ的面积,代入面积公式进行计算即可;
(3)由平行线得出△PCH∽△ACB,求出PH=![]() t,得出PG=6﹣
t,得出PG=6﹣![]() t,连接PM、CM,作MK⊥BC于K点,则四边形GHKM为矩形,得出MK=GH=6,EK=MF=
t,连接PM、CM,作MK⊥BC于K点,则四边形GHKM为矩形,得出MK=GH=6,EK=MF=![]() (6﹣t),则CK=8﹣t﹣
(6﹣t),则CK=8﹣t﹣![]() (6﹣t),由垂直平分线的性质得出PM=CM,由勾股定理得出方程,解方程即可.
(6﹣t),由垂直平分线的性质得出PM=CM,由勾股定理得出方程,解方程即可.
(1)∵四边形ABCD和四边形EFGH是两个全等的矩形,
∴BC=EH=GF=8cm,AB=EF=6cm,∠1B=∠E=∠EFG=90°,
∴AC=FH=![]() =10(cm),
=10(cm),
当CQ∥FH时,△CEQ∽△HEF,
∴![]() ,即
,即![]() ,
,
解得:t=![]() ,
,
即t=![]() 时,CQ∥FH;
时,CQ∥FH;
(2)∵QM⊥FH,
∴∠FNQ=90°=∠EFG,
∴∠QMF+∠MFN=∠MFN+∠EFH=90°,
∴∠QMF=∠EFH,
∴△FMQ∽△EFH,
∴![]() ,即
,即![]() ,
,
解得:MF=![]() (6﹣t),
(6﹣t),
当0<t<6时,五边形GBCQM的面积为y=梯形GBEF的面积﹣△CEQ的面积﹣△MFQ的面积
=![]() (8+8+8﹣t)×6﹣
(8+8+8﹣t)×6﹣![]() ×(8﹣t)×t﹣
×(8﹣t)×t﹣![]() (6﹣t)×
(6﹣t)×![]() (6﹣t)=
(6﹣t)=![]() ,
,
即y与t之间的函数关系式为:![]() ;
;
(3)存在,理由如下:
∵AB∥GH,
∴△PCH∽△ACB,
∴![]() ,即
,即![]() ,
,
∴PH=![]() t,
t,
∴PG=6﹣![]() t,
t,
连接PM、CM,作MK⊥BC于K点,如图2所示:
则四边形GHKM为矩形,
∴MK=GH=6,EK=MF=![]() (6﹣t),
(6﹣t),
∴CK=8﹣t﹣![]() (6﹣t),
(6﹣t),
若M在PC的垂直平分线上,则PM=CM,
由勾股定理得:PM2=PG2+MG2,CM2=CK2+MK2,
∴PG2+MG2=CK2+MK2,
即(6﹣![]() t)2+[8﹣
t)2+[8﹣![]() (6﹣t)]2=62+[8﹣t﹣
(6﹣t)]2=62+[8﹣t﹣![]() (6﹣t)]2,
(6﹣t)]2,
整理得:![]() t2﹣2t=0,
t2﹣2t=0,
解得:t=![]() ,或t=0(不合题意舍去),
,或t=0(不合题意舍去),
∴t=![]() ;
;
即存在某一时刻,使点M在线段PC的中垂线上,t的值为![]() s.
s.



科目:初中数学 来源: 题型:
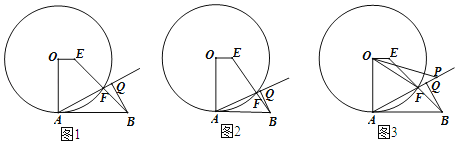
【题目】如图,OA是⊙O的半径,点E为圆内一点,且OA⊥OE,AB是⊙O的切线,EB交⊙O于点F,BQ⊥AF于点Q.
(1)如图1,求证:OE∥AB;
(2)如图2,若AB=AO,求![]() 的值;
的值;
(3)如图3,连接OF,∠EOF的平分线交射线AF于点P,若OA=2,cos∠PAB=![]() ,求OP的长.
,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
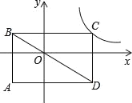
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
A. 16B. ﹣3C. 5D. 5或﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图.
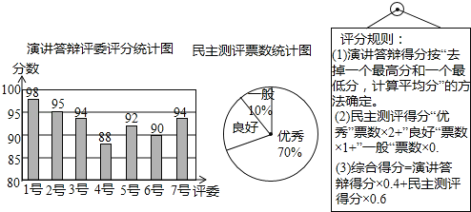
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
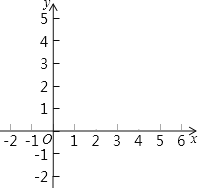
【题目】在平面直角坐标系xOy中,直线y=kx+b(k<0),经过点(6,0),且与坐标轴围成的三角形的面积是9,与函数y=![]() (x>0)的图象G交于A,B两点.
(x>0)的图象G交于A,B两点.
(1)求直线的表达式;
(2)横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.
①当m=2时,直接写出区域W内的整点的坐标 ;
②若区域W内恰有3个整数点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
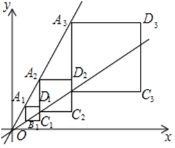
【题目】如图,点A1(1,![]() )在直线y=kx上,过点A1作A1B1∥y轴交直线y=
)在直线y=kx上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=
x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=![]() x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=
x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=![]() x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
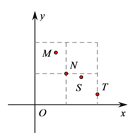
【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中![]() 四位同学的单词记忆效率
四位同学的单词记忆效率![]() 与复习的单词个数
与复习的单词个数![]() 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com