
【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )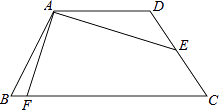
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
【答案】D
【解析】解:如图,延长AE交BC的延长线于G,

∵E为CD中点,
∴CE=DE,
∵AD∥BC,
∴∠DAE=∠G=30°,
在△ADE和△GCE中,
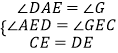 ,
,
∴△ADE≌△GCE(AAS),
∴CG=AD= ![]() ,AE=EG=2
,AE=EG=2 ![]() ,
,
∴AG=AE+EG=2 ![]() +2
+2 ![]() =4
=4 ![]() ,
,
∵AE⊥AF,
∴AF=AGtan30°=4 ![]() ×
× ![]() =4,
=4,
GF=AG÷cos30°=4 ![]() ÷
÷ ![]() =8,
=8,
过点A作AM⊥BC于M,过点D作DN⊥BC于N,
则MN=AD= ![]() ,
,
∵四边形ABCD为等腰梯形,
∴BM=CN,
∵MG=AGcos30°=4 ![]() ×
× ![]() =6,
=6,
∴CN=MG﹣MN﹣CG=6﹣ ![]() ﹣
﹣ ![]() =6﹣2
=6﹣2 ![]() ,
,
∵AF⊥AE,AM⊥BC,
∴∠FAM=∠G=30°,
∴FM=AFsin30°=4× ![]() =2,
=2,
∴BF=BM﹣MF=6﹣2 ![]() ﹣2=4﹣2
﹣2=4﹣2 ![]() .
.
所以答案是:D.
【考点精析】掌握平行线的性质和等腰梯形的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨2000元的原料运回工厂,制成每吨5000元的产品运到B地,已知公路运价为2元/(吨·千米),铁路运价为1.5元/(吨·千米),且这两次运输共支出公路运输费14000元,铁路运输费87000元.

(1)求:该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 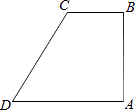
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,双曲线
中,双曲线 ![]() 与直线
与直线 ![]() 交于点A(3,1).
交于点A(3,1).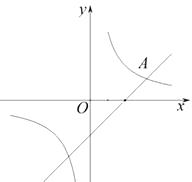
(1)求直线和双曲线的解析式;
(2)直线 ![]() 与x轴交于点B,点P是双曲线
与x轴交于点B,点P是双曲线 ![]() 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线 ![]() 于点D.若DC=2OB,直接写出点
于点D.若DC=2OB,直接写出点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com