
【题目】问题背景
已知在△ABC中,AB边上的动点D由A向B运动(与A、B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.
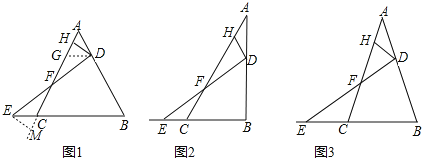
(1)初步尝试
如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等.求证:HF=AH+CF.
小王同学发现可以由以下两种思路解决问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立;
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分);
(2)类比探究
如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是![]() :1,求
:1,求![]() 的值;
的值;
(3)延伸拓展
如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记![]() =m,且点D,E的运动速度相等,试用含m的代数式表示
=m,且点D,E的运动速度相等,试用含m的代数式表示![]() (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
【答案】(1)见解析;(2)![]() =2;(3)
=2;(3)![]() .
.
【解析】
试题分析:(1)过点D作DG∥BC,交AC于点G,先证明△ADG是等边三角形,得出GD=AD=CE,再证明GH=AH,由ASA证明△GDF≌△CEF,得出GF=CF,即可得出结论;
(2)过点D作DG∥BC,交AC于点G,先证出AH=GH=GD,AD=![]() GD,由题意AD=
GD,由题意AD=![]() CE,得出GD=CE,再证明△GDF≌△CEF,得出GF=CF,即可得出结论;
CE,得出GD=CE,再证明△GDF≌△CEF,得出GF=CF,即可得出结论;
(3)过点D作DG∥BC,交AC于点G,先证出 DG=DH=AH,再证明△ADG∽△ABC,△ADG∽△DGH,△DGH∽△ABC,得出![]() =
=![]() =m,
=m,![]() =
=![]() =
=![]() =m,△DGH∽△ABC,得出
=m,△DGH∽△ABC,得出![]() =
=![]() =m,
=m,![]() =m,证明△DFG∽△EFC,得出
=m,证明△DFG∽△EFC,得出![]() =
=![]() =m,
=m,![]() =m,
=m,![]() =
=![]() ,即可得出结果.
,即可得出结果.
(1)证明(选择思路一):过点D作DG∥BC,交AC于点G,如图1所示:
则∠ADG=∠B,∠AGD=∠ACB,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠ADG=∠AGD=∠A,
∴△ADG是等边三角形,
∴GD=AD=CE,
∵DH⊥AC,
∴GH=AH,
∵DG∥BC,
∴∠GDF=∠CEF,∠DGF=∠ECF,
在△GDF和△CEF中,
 ,
,
∴△GDF≌△CEF(ASA),
∴GF=CF,
∴GH+GF=AH+CF,
即HF=AH+CF;
(2)解:过点D作DG∥BC,交AC于点G,如图2所示:
则∠ADG=∠B=90°,
∵∠BAC=∠ADH=30°,
∴∠HGD=∠HDG=60°,
∴AH=GH=GD,AD=![]() GD,
GD,
根据题意得:AD=![]() CE,
CE,
∴GD=CE,
∵DG∥BC,
∴∠GDF=∠CEF,∠DGF=∠ECF,
在△GDF和△CEF中,
 ,
,
∴△GDF≌△CEF(ASA),
∴GF=CF,
∴GH+GF=AH+CF,
即HF=AH+CF,
∴![]() =2;
=2;
(3)解:![]() =
=![]() ,理由如下:
,理由如下:
过点D作DG∥BC,交AC于点G,如图3所示:
则∠ADG=∠B,∠AGD=∠ACB,AD=EC,
∵AB=AC,∠BAC=36°,
∴∠ACB=∠B=∠ADG=∠AGD=72°,
∵∠ADH=∠BAC=36°,
∴AH=GH,∠DHG=72°=∠AGD,
∴DG=DH=AH,△ADG∽△ABC,△ADG∽△DGH,
∴![]() =
=![]() =m,
=m,![]() =
=![]() =
=![]() =m,
=m,
∴△DGH∽△ABC,
∴![]() =
=![]() =m,
=m,
∴![]() =m,
=m,
∵DG∥BC,
∴△DFG∽△EFC,
∴![]() =
=![]() =m,
=m,
∴![]() =m,
=m,
即![]() =m,
=m,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() +1=
+1=![]() .
.





科目:初中数学 来源: 题型:
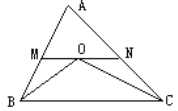
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交与点O, 过点O作MN∥BC,若AB=6,AC=9,则△AMN的周长为_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
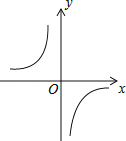
【题目】已知函数y=![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com