
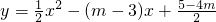 .
.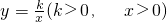 的图象与(2)中的抛物线在第一象限内的交点的横坐标为x0,且满足2<x0<3,求k的取值范围.
的图象与(2)中的抛物线在第一象限内的交点的横坐标为x0,且满足2<x0<3,求k的取值范围. .
.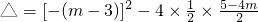 =m2-2m+4=(m-1)2+3.
=m2-2m+4=(m-1)2+3.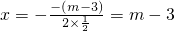 .
.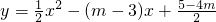 的对称轴为:x=m-3,
的对称轴为:x=m-3, .
. .
.  上,
上, .
. ,y随着x的增大而增大,
,y随着x的增大而增大,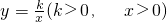 ,y随着x的增大而减小.
,y随着x的增大而减小. >
>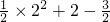 ,
, >
> ,
, ,进而求出m的值,即可得出二次函数解析式,即可得出n的值;
,进而求出m的值,即可得出二次函数解析式,即可得出n的值; ,y随着x的增大而增大,再利用x=2和3时y的值得出k的取值范围.
,y随着x的增大而增大,再利用x=2和3时y的值得出k的取值范围.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:福建省中考真题 题型:解答题
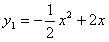
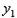 的顶点坐标.
的顶点坐标. 线
线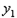 向右平移2个单位,再向上平移1个单位,得到抛物线
向右平移2个单位,再向上平移1个单位,得到抛物线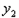 ,求抛物线
,求抛物线 的解析式.
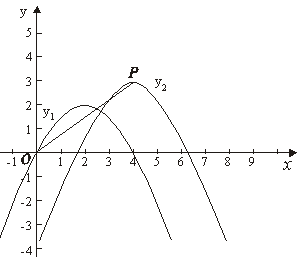
的解析式.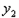 的顶点为P,
的顶点为P,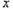 轴上有一动点M,在
轴上有一动点M,在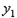 、
、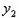 这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由
这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由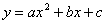 (
(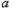 ≠0)的对称轴是
≠0)的对称轴是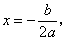 顶点坐标是
顶点坐标是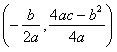 ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
(11分)如图,已知抛物线![]()
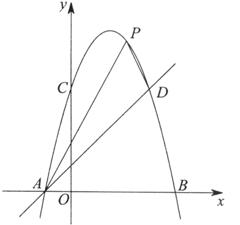
1.(1)求这条抛物线的解析式;
2.(2)![]() 点P的横坐标是m,且
点P的横坐标是m,且![]() 值;
值;
3.(3)点M是直线AD上一动点,直线写出使△ACM为等腰三角形的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知抛物线![]() 的解析式为
的解析式为![]()
⑴求抛物线![]() 的顶点坐标;
的顶点坐标;
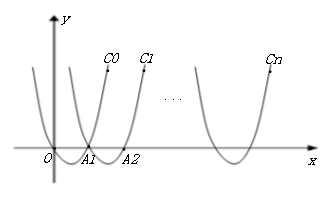
⑵将抛物线![]() 每次向右平移2个单位,平移n次,依次得到抛物线
每次向右平移2个单位,平移n次,依次得到抛物线![]() (n为正整数)
(n为正整数)
① 求抛物线![]() 与x轴的交点A1、A2的坐标;
与x轴的交点A1、A2的坐标;
② 试确定抛物线![]() 的解析式.(直接写出答案,不需要解题过程)
的解析式.(直接写出答案,不需要解题过程)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省泰州市九年级下学期质量检测数学卷 题型:解答题
(本题满分8分)在平面直角坐标系中,抛物线交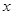 轴于
轴于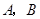 两点,交
两点,交 轴于点
轴于点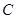 ,已知抛物线的对称轴为
,已知抛物线的对称轴为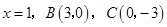 .求这个抛物线的解析式。
.求这个抛物线的解析式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com