
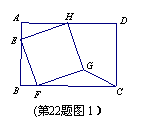
已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
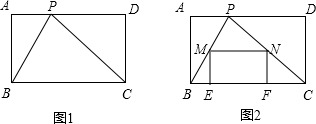
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.

解:(1)如图①,过点G作![]() 于M.
于M.
在正方形EFGH中,
![]() .
.
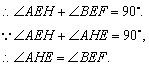
又∵![]() ,
,
∴⊿AHE≌⊿BEF. ………………………2分
同理可证:⊿MFG≌⊿BEF.
∴GM=BF=AE=2.
∴FC=BC-BF=10.
(2)如图②,过点G作![]() 于M.连接HF.
于M.连接HF.
![]()
![]()
又![]()
∴⊿AHE≌⊿MFG.
∴GM=AE=2.
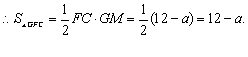
(3)⊿GFC的面积不能等于2.
∵若![]() 则12- a =2,∴a=10.
则12- a =2,∴a=10.
此时,在⊿BEF中,
![]()
在⊿AHE中,
![]() .
.
∴AH>AD.
即点H已经不在边AB上.
故不可能有![]()
解法二:⊿GFC的面积不能等于2.
∵点H在AD上,
∴菱形边长EH的最大值为![]() .
.
∴BF的最大值为![]() .
.
又因为函数![]() 的值随着a的增大而减小,
的值随着a的增大而减小,
所以![]() 的最小值为
的最小值为![]() .
.
又∵![]() ,∴⊿GFC的面积不能等于2.
,∴⊿GFC的面积不能等于2.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 |
| 3 |
| 16 |
| 3 |
| 8 |
| 3 |
| 16 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com