
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下 :
:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)计算上述试验中“4朝下”的频率是多少?
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是 ![]() .”的说法正确吗?为什么?
.”的说法正确吗?为什么?
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
【答案】
(1)
“4朝下”的频率: ![]() ;…
;…
故答案为: ![]() .
.
(2)
这种说法是错误的.在60次试验中,“2朝下”的频率为 ![]() .
.
并不能说明“2朝下”这一事件发生的概率为 ![]() .只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
.只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
(3)
随机投掷正四面体两次,所有可能出现的结果如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
总共有16种结果,每种结果出现的可能性相同,而两次朝下数字之和大于4的结果有10种.
∴P(朝下数字之和大于4)= ![]()
【解析】本题主要考查列表法与树状图法求概率,以及频率的意义,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.(1)先由频率=频数÷试验次数算出频率;(2)根据表格观察抛掷的次数增多时,频率稳定到哪个数值,这就是概率.(3)列表列举出所有的可能的结果,然后利用概率公式解答即可.
【考点精析】掌握用频率估计概率是解答本题的根本,需要知道在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.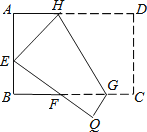
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( ).
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a,b,c;A,B,N,E,F五点在同一直线上,则c=(用含有a,b的代数式表示). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com