
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþy£Ω![]() x2©Å
x2©Å![]() x©Å4Ωªx÷·”⁄A°¢B¡Ωµ„£¨Ωªy÷·”⁄µ„C.
x©Å4Ωªx÷·”⁄A°¢B¡Ωµ„£¨Ωªy÷·”⁄µ„C.
(1)µ„PŒ™œþ∂ŒBCœ¬∑Ω≈◊ŒÔœþ…œµƒ»Œ“‚“ªµ„£¨“ª∂ص„G¥”µ„P≥ˆ∑¢—ÿ µ±¬∑æ∂“‘√ø√Î1∏ˆµ•Œª≥§∂»‘À∂صΩy÷·…œ“ªµ„M£¨‘Ÿ—ÿ µ±¬∑æ∂“‘√ø√Î1∏ˆµ•Œª≥§∂»‘À∂صΩx÷·…œµƒµ„N£¨‘Ÿ—ÿx÷·“‘√ø√Î![]() ∏ˆµ•Œª≥§∂»‘À∂ØµΩµ„B.µ±Àƒ±þ–ŒACPB√ʪ˝◊Ó¥Û ±£¨«Û‘À∂Ø ±º‰tµƒ◊Ó–°÷µ£ª
∏ˆµ•Œª≥§∂»‘À∂ØµΩµ„B.µ±Àƒ±þ–ŒACPB√ʪ˝◊Ó¥Û ±£¨«Û‘À∂Ø ±º‰tµƒ◊Ó–°÷µ£ª
(2)π˝µ„C◊˜ACµƒ¥πœþΩªx÷·”⁄µ„D£¨Ω´°˜AOC»∆µ„O–˝◊™£¨–˝◊™∫Ûµ„A°¢Cµƒ∂‘”¶µ„∑÷±Œ™A1°¢C1£¨‘⁄–˝◊™π˝≥Ã÷–÷±œþA1C1”Îx÷·Ωª”⁄µ„Q.”Îœþ∂ŒCDΩª”⁄µ„I.µ±°˜DQI «µ»—¸»˝Ω«–Œ ±£¨÷±Ω”–¥≥ˆDQµƒ≥§∂».

°æ¥∞∏°ø(1)tµƒ◊Ó–°÷µŒ™![]() £ª(2)DQµƒ≥§∂»Œ™
£ª(2)DQµƒ≥§∂»Œ™![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() ©Å
©Å![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() .
.
°æΩ‚Œˆ°ø
(1)π˝µ„B◊˜BK°ÕBCΩªy÷·”⁄µ„K£¨◊˜P°‰H°ÕBKΩªBK”⁄µ„H°¢Ωªy÷·”⁄µ„M°¢Ωªx÷·”⁄µ„N£¨‘Ú¥À ±‘À∂صƒ ±º‰◊Ó–°£¨º¥ø…«ÛΩ‚£ª
(2)Ω´°˜AOC»∆µ„O–˝◊™£¨œýµ±”⁄¥Ê‘⁄“ª∏ˆ∞Îæ∂Œ™OR‘≤O£¨‘⁄’˚∏ˆ–˝◊™π˝≥Ã÷–£¨AC º÷’Œ™¥π÷±”⁄ORµƒ«–œþ£¨»∑∂®‘≤µƒ∞Îæ∂OR∫Û£¨∑÷ORøøΩ¸x÷·°¢y÷·¡Ω÷÷¥Û«Èøˆ£¨∑÷±‘⁄Àƒ∏ˆœÛœÞ÷¥Œ«ÛΩ‚º¥ø….
Ω‚£∫(1)◊˜PS°Œy÷·ΩªBC”⁄S£¨
y£Ω![]() x2©Å
x2©Å![]() x©Å4£¨¡Óx£Ω0£¨‘Úy£Ω©Å4£¨¡Óy£Ω0£¨‘Úx£Ω-3ªÚ4£¨
x©Å4£¨¡Óx£Ω0£¨‘Úy£Ω©Å4£¨¡Óy£Ω0£¨‘Úx£Ω-3ªÚ4£¨
𠵄A°¢B°¢Cµƒ◊¯±Í∑÷±Œ™(©Å3£¨0)°¢(4£¨0)°¢(0£¨©Å4)£¨
‘Ú÷±œþBCµƒ±Ì¥Ô ΩŒ™£∫y£Ωx©Å4£¨
SÀƒ±þ–ŒACPB£ΩS°˜ABC+S°˜PBC£¨
°þS°˜ABCŒ™≥£ ˝£¨
°ý÷ª“™S°˜PBC»°µ√◊Ó¥Û÷µ£¨Àƒ±þ–ŒACPB√ʪ˝º¥Œ™◊Ó¥Û£¨
…˵„P(x£¨![]() x2©Å
x2©Å![]() x©Å4)£¨‘Úµ„S(x£¨x©Å4)£¨
x©Å4)£¨‘Úµ„S(x£¨x©Å4)£¨
S°˜PBC£Ω![]() °¡PS°¡OB£Ω
°¡PS°¡OB£Ω![]() °¡4°¡(x©Å4©Å
°¡4°¡(x©Å4©Å![]() x2+
x2+![]() x+4)£Ω
x+4)£Ω![]() x2+
x2+![]() x£¨
x£¨
°þ![]() <0£¨‘ÚS°˜PBC”–◊Ó¥Û÷µ£¨º¥Àƒ±þ–ŒACPB√ʪ˝”–◊Ó¥Û÷µ£¨
<0£¨‘ÚS°˜PBC”–◊Ó¥Û÷µ£¨º¥Àƒ±þ–ŒACPB√ʪ˝”–◊Ó¥Û÷µ£¨
¥À ±£¨x£Ω2£¨π µ„P(2£¨©Å![]() ).
).
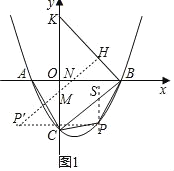
◊˜µ„Pπÿ”⁄y÷·µƒ∂‘≥∆µ„P°‰(©Å2£¨©Å![]() )£¨
)£¨
π˝µ„B◊˜BK°ÕBCΩªy÷·”⁄µ„K£¨◊˜P°‰H°ÕBKΩªBK”⁄µ„H°¢Ωªy÷·”⁄µ„M°¢Ωªx÷·”⁄µ„N£¨
‘Ú¥À ±‘À∂صƒ ±º‰◊Ó–°£¨
t£ΩP°‰M+MN+![]() BN£ΩPM+MN+HN£¨
BN£ΩPM+MN+HN£¨
÷±œþBK°ÕBC£¨‘Ú÷±œþBKµƒ±Ì¥Ô ΩŒ™£∫y£Ω©Åx+b£¨
Ω´µ„Bµƒ◊¯±Í¥˙»Î…œ Ω≤¢Ω‚µ√£∫
÷±œþBKµƒ±Ì¥Ô ΩŒ™£∫y£Ω©Åx+4°≠¢Ÿ£¨
Õ¨¿Ìø…µ√÷±œþP°‰Hµƒ±Ì¥Ô ΩŒ™£∫y£Ωx©Å![]() °≠¢⁄£¨
°≠¢⁄£¨
¡™¡¢¢Ÿ¢⁄≤¢Ω‚µ√£∫x£Ω![]() £¨
£¨
𠵄H(![]() £¨
£¨![]() )£¨
)£¨
‘Út£ΩP°‰H£Ω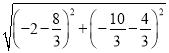 £Ω
£Ω![]() £¨
£¨
π ‘À∂Ø ±º‰tµƒ◊Ó–°÷µŒ™![]() £ª
£ª
(2)°þAC°ÕAD£¨
‘Ú÷±œþCDµƒ±Ì¥Ô ΩŒ™£∫y£Ω![]() x©Å4£¨
x©Å4£¨
𠵄D(![]() £¨0)£ª
£¨0)£ª
»ÁÕº2£¨π˝µ„O◊˜OR°ÕAC”⁄µ„R£¨
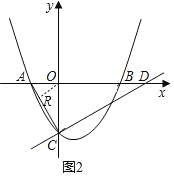
”…√ʪ˝π´ Ωµ√£∫![]() OR°¡AC£Ω
OR°¡AC£Ω![]() OA°¡OC£¨
OA°¡OC£¨
º¥£∫OR£Ω![]() £Ω
£Ω![]() £¨
£¨
…Ë°œODC£Ω¶¡£¨‘Útan¶¡£Ω![]() £¨sin¶¡£Ω
£¨sin¶¡£Ω![]() £¨
£¨
‘Útan2¶¡£Ω![]() £¨tan
£¨tan![]() £Ω
£Ω![]() (÷§√˜º˚±∏◊¢)£¨
(÷§√˜º˚±∏◊¢)£¨
«Èøˆ“ª£∫µ±ORøøΩ¸y÷· ±£¨
¢Ÿµ±OR‘⁄“ª°¢»˝œÛœÞ ±£¨»ÁÕº3£¨4£∫
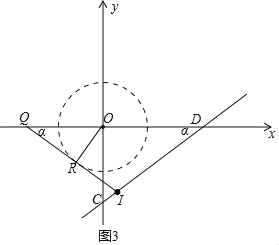
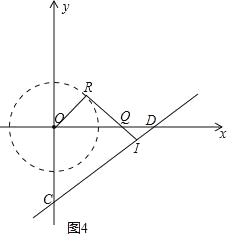
‘⁄Õº3÷–£¨IQ£ΩID£¨
‘ÚOQ£Ω![]() £Ω
£Ω![]() £Ω4£¨
£Ω4£¨
π QD£Ω![]() +4£Ω
+4£Ω![]() £ª
£ª
‘⁄Õº4÷–£¨IQ£ΩID£¨
Õ¨¿ÌQD£Ω![]() ©Å4£Ω
©Å4£Ω![]() £ª
£ª
¢⁄µ±OR‘⁄∂˛°¢ÀƒœÛœÞ ±£¨»ÁÕº5£¨6£∫
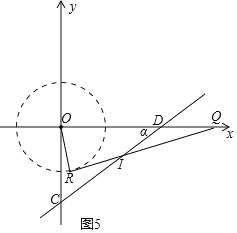
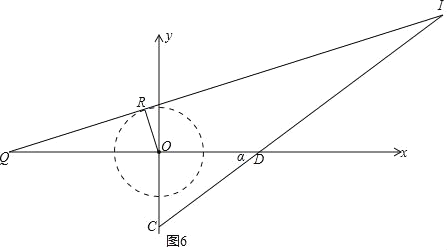
‘⁄Õº5÷–£¨DI£ΩDQ£¨
‘Ú°œDQI£Ω°œDIQ£Ω![]() °œODC£Ω
°œODC£Ω![]() ¶¡£¨
¶¡£¨
OQ£Ω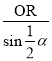 £Ω
£Ω![]() £¨
£¨
‘ÚDQ£Ω![]() ©Å
©Å![]() £¨
£¨
‘⁄Õº6÷–£¨ «”Îœþ∂ŒCDµƒ—”≥§œþœýΩª£¨≤ª∑˚∫œÃ‚“‚£ª
«Èøˆ∂˛£∫µ±ORøøΩ¸x÷· ±£¨
»Áœ¬Õº£∫µ±µ„R‘⁄∂˛°¢ÀƒœÛœÞ ±£¨»ÁÕº7£¨
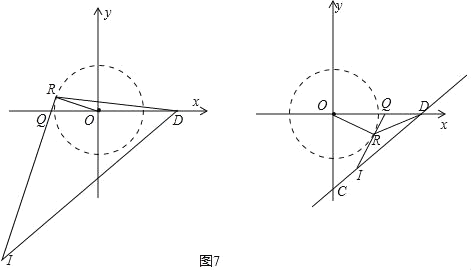
º˚◊Û≤ýÕº£¨ «”Îœþ∂ŒDCµƒ—”≥§œþœýΩª£¨≤ª∑˚∫œÃ‚“‚£ª
º˚”“≤ýÕº£¨Õ¨¿Ìø…µ√£∫DQ£Ω![]() ©Å
©Å![]() £Ω
£Ω![]() £ª
£ª
µ±µ„R‘⁄“ª°¢»˝œÛœÞ ±£¨»ÁÕº8£¨
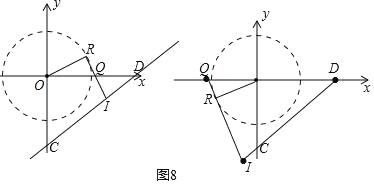
º˚◊Û≤ýÕº£¨Õ¨¿Ìø…µ√£∫DQ£Ω![]() ©Å
©Å![]()
º˚”“≤ýÕº£¨ «”Îœþ∂ŒDCµƒ—”≥§œþœýΩª£¨≤ª∑˚∫œÃ‚“‚£ª
◊€…œÀ˘ ˆ£¨DQµƒ≥§∂»Œ™![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() ©Å
©Å![]() ªÚ
ªÚ![]() +
+![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() .
.
±∏◊¢£∫“—÷™tan¶¡£Ω![]() £¨«Ûtan2¶¡∫Õtan
£¨«Ûtan2¶¡∫Õtan![]() .
.
»ÁÕº°˜ABD «“‘BDŒ™µ◊µƒµ»—¸»˝Ω«–Œ£¨AC°ÕBD£¨π˝µ„D◊˜DH°ÕAB£¨
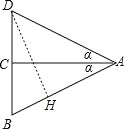
‘Ú…Ë£∫°œDAC£Ω°œBAC£Ω¶¡£¨tan¶¡£Ω![]() £¨…ËBC£ΩCD£Ω3a£¨‘ÚAC£Ω4a£¨
£¨…ËBC£ΩCD£Ω3a£¨‘ÚAC£Ω4a£¨
”…»˝Ω«–Œµƒ√ʪ˝π´ Ωµ√£∫![]() AH°¡AB£Ω
AH°¡AB£Ω![]() DB°¡AC£¨
DB°¡AC£¨
Ω‚µ√£∫AH£Ω![]() £Ω
£Ω![]() £¨
£¨
‘Úsin2¶¡£Ωsin°œBAD£Ω![]() £Ω
£Ω![]() £¨tan2¶¡£Ω
£¨tan2¶¡£Ω![]() £¨
£¨
Õ¨¿Ìø…µ√£∫tan![]()
![]() £Ω
£Ω![]() .
.


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨≈◊ŒÔœþy=ax2+2ax©Å3a£®a£æ0£©”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£Æ
£®1£©«Û≈◊ŒÔœþµƒ∂‘≥∆÷·º∞œþ∂ŒABµƒ≥§£ª
£®2£©≈◊ŒÔœþµƒ∂•µ„Œ™P£¨»Ù°œAPB=120°„£¨«Û∂•µ„Pµƒ◊¯±Íº∞aµƒ÷µ£ª
£®3£©»Ù‘⁄≈◊ŒÔœþ…œ¥Ê‘⁄“ªµ„N£¨ πµ√°œANB=90°„£¨Ω·∫œÕºœÛ£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
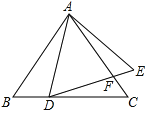
°æƒø°ø»ÁÕº£¨“—÷™°˜ABC∫Õ°˜ADEæ˘Œ™µ»±þ»˝Ω«–Œ£¨D‘⁄BC…œ£¨DE”ÎACœýΩª”⁄µ„F£¨BD=3£¨CF=2,‘Ú°˜ADEµƒ÷Ð≥§=________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
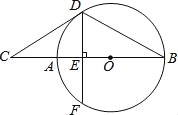
°æƒø°ø»ÁÕº£¨AB «‘≤Oµƒ÷±æ∂£¨µ„C‘⁄BAµƒ—”≥§œþ…œ£¨÷±œþCD”Α≤Oœý«–”⁄µ„D£¨œ“DF°ÕAB”⁄µ„E£¨¡¨Ω”BD£¨CD£ΩBD£Ω4![]() £¨‘ÚOEµƒ≥§∂»Œ™( )
£¨‘ÚOEµƒ≥§∂»Œ™( )
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—◊»»µƒœƒÃÏ¿¥¡Ÿ÷ƺ .Œ™¡Àµ˜≤ÈŒ“–£—ß…˙œ˚∑¿∞≤»´÷™ ∂ÀÆ∆Ω£¨—ß–£◊È÷Ø¡À“ª¥Œ»´–£µƒœ˚∑¿∞≤»´÷™ ∂≈ý—µ£¨≈ý—µÕÍ∫ÛΩ¯––≤‚ ‘£¨‘⁄»´–£2400√˚—ß…˙÷–£¨∑÷±≥È»°¡Àƒ–…˙£¨≈Æ…˙∏˜15∑ð≥…º®£¨’˚¿Ì∑÷Œˆπ˝≥ûÁœ¬£¨«Î≤π≥‰ÕÍ’˚.
£® ’ºØ ˝æð£©
ƒ–…˙15√˚—ß…˙≤‚ ‘≥…º®Õ≥º∆»Áœ¬£∫
68£¨72£¨89£¨85£¨82£¨85£¨74£¨92£¨80£¨85£¨76£¨85£¨69£¨78£¨80
≈Æ…˙15√˚—ß…˙≤‚ ‘≥…º®Õ≥º∆»Áœ¬£∫(¬˙∑÷100∑÷)
82£¨88£¨83£¨76£¨73£¨78£¨67£¨81£¨82£¨80£¨80£¨86£¨82£¨80£¨82
∞¥»Áœ¬∑÷ ˝∂Œ’˚¿Ì°¢√Ë ˆ’‚¡Ω◊È—˘±æ ˝æð£∫
◊ȱ ∆µ ˝ | 65.5°´70.5 | 70.5°´75.5 | 75.5°´80.5 | 80.5°´85.5 | 85.5°´90.5 | 90.5°´95.5 |
ƒ–…˙ | 2 | 2 | 4 | 5 | 1 | 1 |
≈Æ…˙ | 1 | 1 | 5 | 6 | 2 | 0 |
£®∑÷Œˆ ˝æð£©
(1)¡Ω◊È—˘±æ ˝æðµƒ∆Ωæ˘ ˝°¢÷⁄ ˝°¢÷–Œª ˝°¢∑Ω≤Ó»Áœ¬±ÌÀ˘ æ£∫
∞ýº∂ | ∆Ωæ˘ ˝ | ÷⁄ ˝ | ÷–Œª ˝ | ∑Ω≤Ó |
ƒ–…˙ | 80 | x | 80 | 45.9 |
≈Æ…˙ | 80 | 82 | y | 24.3 |
‘⁄±Ì÷–£∫x£Ω_____£ªy£Ω_____.
(2)»ÙπÊ∂®µ√∑÷‘⁄80∑÷“‘…œ(≤ª∫¨80∑÷)Œ™∫œ∏Ò£¨«Îπ¿º∆»´–£—ß…˙÷–œ˚∑¿∞≤»´÷™ ∂∫œ∏Òµƒ—ß…˙”–______»À.
(3)Õ®π˝ ˝æð∑÷Œˆµ√µΩµƒΩ·¬€ «≈Æ…˙’∆Œ’œ˚∑¿∞≤»´œýπÿ÷™ ∂µƒ’˚ÃÂÀÆ∆Ω±»ƒ–…˙∫√£¨«Î¥”¡Ω∏ˆ∑Ω√ÊÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABD”ΰ˜AEC∂º «µ»±þ»˝Ω«–Œ£¨AB°ŸAC£Æœ¬¡–Ω·¬€÷–£¨’˝»∑µƒ « £Æ¢ŸBE£ΩCD£ª¢⁄°œBOD£Ω60£ª¢€°˜BOD°◊°˜COE£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥≥¨ –œ˙ €“ª÷÷Œƒæþ£¨Ω¯º€Œ™5‘™/º˛£Æ €º€Œ™6‘™/º˛ ±£¨µ±Ãϵƒœ˙ €¡øŒ™100º˛£Æ‘⁄œ˙ €π˝≥Ã÷–∑¢œ÷£∫ €º€√ø…œ’«0.5‘™£¨µ±Ãϵƒœ˙ €¡øæÕºı…Ÿ5º˛£Æ…˵±ÃÏœ˙ €µ•º€Õ≥“ªŒ™![]() ‘™/º˛£®
‘™/º˛£®![]() £¨«“
£¨«“![]() «∞¥0.5‘™µƒ±∂ ˝…œ’«£©£¨µ±ÃÏœ˙ €¿˚»ÛŒ™
«∞¥0.5‘™µƒ±∂ ˝…œ’«£©£¨µ±ÃÏœ˙ €¿˚»ÛŒ™![]() ‘™£Æ
‘™£Æ
£®1£©«Û![]() ”Î
”Î![]() µƒ∫Ø ˝πÿœµ Ω£®≤ª“™«Û–¥≥ˆ◊‘±‰¡øµƒ»°÷µ∑∂Œß£©£ª
µƒ∫Ø ˝πÿœµ Ω£®≤ª“™«Û–¥≥ˆ◊‘±‰¡øµƒ»°÷µ∑∂Œß£©£ª
£®2£©“™ πµ±ÃÏœ˙ €¿˚»Û≤ªµÕ”⁄240‘™£¨«Ûµ±ÃÏœ˙ €µ•º€À˘‘⁄µƒ∑∂Œß£ª
£®3£©»Ù√øº˛Œƒæþµƒ¿˚»Û≤ª≥¨π˝![]() £¨“™œÎµ±ÃϪҵ√¿˚»Û◊Ó¥Û£¨√øº˛Œƒæþ €º€Œ™∂ý…Ÿ‘™£ø≤¢«Û≥ˆ◊Ó¥Û¿˚»Û£Æ
£¨“™œÎµ±ÃϪҵ√¿˚»Û◊Ó¥Û£¨√øº˛Œƒæþ €º€Œ™∂ý…Ÿ‘™£ø≤¢«Û≥ˆ◊Ó¥Û¿˚»Û£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Àƒ±þ–ŒABCD÷–£¨E£¨F∑÷± «AB£¨AD±þ…œµƒµ„£¨DE”ÎCFΩª”⁄µ„G.
(1)»ÁÕº¢Ÿ£¨»ÙÀƒ±þ–ŒABCD «æÿ–Œ£¨«“DE°ÕCF£¨«Û÷§£∫![]() £ª
£ª
(2)»ÁÕº¢⁄£¨»ÙÀƒ±þ–ŒABCD «∆Ω––Àƒ±þ–Œ£¨ ‘ÃΩæø£∫µ±°œB”ΰœEGC¬˙◊„ ≤√¥πÿœµ ±£¨ πµ√![]() ≥…¡¢£ø≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
≥…¡¢£ø≤¢÷§√˜ƒ„µƒΩ·¬€£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ƒ≥–£ ˝—ß–À»§–°◊ÈŒ™≤‚¡ø–£‘∞÷˜Ω×߬•ABµƒ∏þ∂»£¨”…”⁄Ω×߬•µ◊≤ø≤ªƒÐ÷±Ω”µΩ¥Ô£¨π –À»§–°◊È‘⁄∆Ωµÿ…œ—°‘Ò“ªµ„C£¨”√≤‚Ω«∆˜≤‚µ√÷˜Ω×߬•∂•∂ÀAµƒ—ˆΩ«Œ™30°„£¨‘ŸœÚ÷˜Ω×߬•µƒ∑ΩœÚ«∞Ω¯24√◊£¨µΩ¥Ôµ„E¥¶£®C£¨E£¨B»˝µ„‘⁄Õ¨“ª÷±œþ…œ£©£¨”÷≤‚µ√÷˜Ω×߬•∂•∂ÀAµƒ—ˆΩ«Œ™60°„£¨“—÷™≤‚Ω«∆˜CDµƒ∏þ∂»Œ™1.6√◊£¨«Îº∆À„÷˜Ω×߬•ABµƒ∏þ∂»£Æ£®![]() °÷1.73£¨Ω·π˚æ´»∑µΩ0.1√◊£©
°÷1.73£¨Ω·π˚æ´»∑µΩ0.1√◊£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com