
ЎҫМвДҝЎҝИзНјЈ¬¶юҙОәҜКэ![]() өДНјПсУл
өДНјПсУл![]() ЦбҪ»УЪ
ЦбҪ»УЪ![]() Ўў
Ўў![]() БҪөгЈ¬Ул
БҪөгЈ¬Ул![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() Ј¬
Ј¬![]() Ј®өг
Ј®өг![]() ФЪәҜКэНјПсЙПЈ¬
ФЪәҜКэНјПсЙПЈ¬![]() ЦбЈ¬ЗТ
ЦбЈ¬ЗТ![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() КЗЕЧОпПЯөД¶ФіЖЦбЈ¬
КЗЕЧОпПЯөД¶ФіЖЦбЈ¬![]() КЗЕЧОпПЯөД¶ҘөгЈ®
КЗЕЧОпПЯөД¶ҘөгЈ®
ЈЁ1Ј©Зу![]() Ўў
Ўў![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ИзНјўЩЈ¬Б¬ҪУ![]() Ј¬ПЯ¶О
Ј¬ПЯ¶О![]() ЙПөДөг
ЙПөДөг![]() №ШУЪЦұПЯ
№ШУЪЦұПЯ![]() өД¶ФіЖөг
өД¶ФіЖөг![]() ЗЎәГФЪПЯ¶О
ЗЎәГФЪПЯ¶О![]() ЙПЈ¬Зуөг
ЙПЈ¬Зуөг![]() өДЧшұкЈ»
өДЧшұкЈ»
ЈЁ3Ј©ИзНјўЪЈ¬¶Ҝөг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬№эөг
ЙПЈ¬№эөг![]() Чч
Чч![]() ЦбөДҙ№ПЯ·ЦұрУл
ЦбөДҙ№ПЯ·ЦұрУл![]() Ҫ»УЪөг
Ҫ»УЪөг![]() Ј¬УлЕЧОпПЯҪ»УЪөг
Ј¬УлЕЧОпПЯҪ»УЪөг![]() Ј®КФОКЈәЕЧОпПЯЙПКЗ·сҙжФЪөг
Ј®КФОКЈәЕЧОпПЯЙПКЗ·сҙжФЪөг![]() Ј¬К№өГ
Ј¬К№өГ![]() Ул
Ул![]() өДГж»эПаөИЈ¬ЗТПЯ¶О
өДГж»эПаөИЈ¬ЗТПЯ¶О![]() өДіӨ¶ИЧоРЎЈҝИз№ыҙжФЪЈ¬Зуіцөг
өДіӨ¶ИЧоРЎЈҝИз№ыҙжФЪЈ¬Зуіцөг![]() өДЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
өДЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј»ЈЁ2Ј©өг
Ј»ЈЁ2Ј©өг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() Ј»ЈЁ3Ј©өг
Ј»ЈЁ3Ј©өг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() әН
әН![]()
ЎҫҪвОцЎҝ
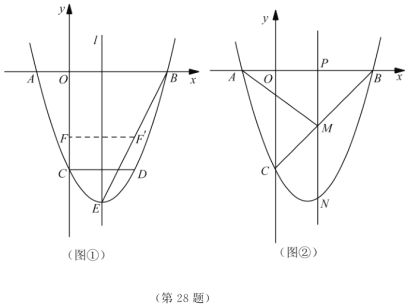
КФМв·ЦОцЈә ЈЁ1Ј©ёщҫЭ¶юҙОәҜКэөД¶ФіЖЦṫКҪЈ¬ЕЧОпПЯЙПөДөгҙъИлЈ¬јҙҝЙЈ»ЈЁ2Ј©ПИЗуFөД¶ФіЖөгЈ¬ҙъИлЦұПЯBEЈ¬јҙҝЙЈ»ЈЁ3Ј©№№ФмРВөД¶юҙОәҜКэЈ¬АыУГЖдРФЦКЗуј«Цө.
КФМвҪвОцЈә.ҪвЈәЈЁ1Ј©![]() ЦбЈ¬
ЦбЈ¬![]() Ј¬
Ј¬![]() ЕЧОпПЯ¶ФіЖЦбОӘЦұПЯ
ЕЧОпПЯ¶ФіЖЦбОӘЦұПЯ![]()
![]()
![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]()
![]() ҪвөГ
ҪвөГ![]() »т
»т![]() ЈЁЙбИҘЈ©Ј¬
ЈЁЙбИҘЈ©Ј¬![]()
ЈЁ2Ј©Йиөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]()
![]() ¶ФіЖЦбОӘЦұПЯ
¶ФіЖЦбОӘЦұПЯ![]() өг
өг![]() №ШУЪЦұПЯ
№ШУЪЦұПЯ![]() өД¶ФіЖөг
өД¶ФіЖөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() .
.
![]() ЦұПЯ
ЦұПЯ![]() ҫӯ№эөг
ҫӯ№эөг![]() АыУГҙэ¶ЁПөКэ·ЁҝЙөГЦұПЯ
АыУГҙэ¶ЁПөКэ·ЁҝЙөГЦұПЯ![]() өДұнҙпКҪОӘ
өДұнҙпКҪОӘ![]() .
.
ТтОӘөг![]() ФЪ
ФЪ![]() ЙПЈ¬
ЙПЈ¬![]()
![]() јҙөг
јҙөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]()
ЈЁ3Ј©ҙжФЪөг![]() ВъЧгМвТв.Йиөг
ВъЧгМвТв.Йиөг![]() ЧшұкОӘ
ЧшұкОӘ![]() Ј¬Фт
Ј¬Фт![]()
Чч![]() ҙ№ЧгОӘ
ҙ№ЧгОӘ![]()
![]()
![]()
ўЩөг![]() ФЪЦұПЯ
ФЪЦұПЯ![]() өДЧуІаКұЈ¬
өДЧуІаКұЈ¬![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]()
![]() ФЪ
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() КұЈ¬
КұЈ¬![]() ИЎЧоРЎЦө
ИЎЧоРЎЦө![]() .ҙЛКұ
.ҙЛКұ![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]()
ўЪөг![]() ФЪЦұПЯ
ФЪЦұПЯ![]() өДУТІаКұЈ¬
өДУТІаКұЈ¬![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]() Н¬АнЈ¬
Н¬АнЈ¬![]() КұЈ¬
КұЈ¬![]() ИЎЧоРЎЦө
ИЎЧоРЎЦө![]() .ҙЛКұ
.ҙЛКұ![]() өгөДЧшұкОӘ
өгөДЧшұкОӘ![]()
ЧЫЙПЛщКцЈәВъЧгМвТвөГөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() әН
әН![]()


 Н¬ІҪБ·П°Зҝ»ҜНШХ№ПөБРҙр°ё
Н¬ІҪБ·П°Зҝ»ҜНШХ№ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁұҫМвВъ·Ц8·ЦЈ©
ИзНјЈ¬ЦұПЯ![]() УлЛ«ЗъПЯ
УлЛ«ЗъПЯ![]() ЈЁ
ЈЁ![]() ОӘіЈКэЈ¬
ОӘіЈКэЈ¬![]() Ј©ФЪөЪТ»ПуПЮДЪҪ»УЪөг
Ј©ФЪөЪТ»ПуПЮДЪҪ»УЪөг![]() Ј¬ЗТУл
Ј¬ЗТУл![]() ЦбЎў
ЦбЎў![]() Цб·ЦұрҪ»УЪ
Цб·ЦұрҪ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ®
БҪөгЈ®
ЈЁ1Ј©ЗуЦұПЯәНЛ«ЗъПЯөДҪвОцКҪЈ»
ЈЁ2Ј©өг![]() ФЪ
ФЪ![]() ЦбЙПЈ¬ЗТ
ЦбЙПЈ¬ЗТ![]() өДГж»эөИУЪ
өДГж»эөИУЪ![]() Ј¬Зу
Ј¬Зу![]() өгөДЧшұкЈ®
өгөДЧшұкЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРЛө·ЁІ»ХэИ·өДКЗЈЁ Ј©
A.Ў°ДіЙд»чФЛ¶ҜФұЙд»чТ»ҙОЈ¬ХэЦР°РРДЎұКфУЪЛж»ъКВјю
B.Ў°13ГыН¬С§ЦБЙЩУРБҪГыН¬С§өДіцЙъФВ·ЭКЗПаН¬өДЎұКфУЪұШИ»КВјю
C.Ў°ФЪұкЧјҙуЖшС№ПВЈ¬өұОВ¶ИҪөөҪ-5ЎжКұЈ¬Л®ҪбіЙұщЎұКфУЪЛж»ъКВјю
D.Ў°ДіҙьЦРУР8ёцЦКөШҫщФИөДЗтЈ¬ЗТ¶јКЗәмЗтЈ¬ИОТвГюіцТ»ЗтКЗ°ЧЗтЎұКфУЪІ»ҝЙДЬКВјю
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬УРөгЈЁ©Ғ2Ј¬a+3Ј©Ј¬BЈЁbЈ¬b©Ғ3Ј©Ј®
ЈЁ1Ј©өұөгAФЪөЪ¶юПуПЮөДҪЗЖҪ·ЦПЯЙПКұЈ¬ЗуaөДЦөЈ»
ЈЁ2Ј©өұөгBөҪxЦбөДҫаАлКЗЛьөҪyЦбөДҫаАл2ұ¶КұЈ¬ЗуөгBЛщФЪөДПуПЮО»ЦГЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝіхТ»ЈЁ1Ј©°аХл¶ФЎ°ДгЧоПІ°®өДҝОНв»о¶ҜПоДҝЎұ¶ФИ«°аС§ЙъҪшРРөчІйЈЁГҝГыС§Йъ·ЦұрСЎТ»ёц»о¶ҜПоДҝЈ©Ј¬ІўёщҫЭөчІйҪб№ыБРіцНіјЖұнЈ¬»жЦЖіЙЙИРОНіјЖНјЈ®

ёщҫЭТФЙПРЕПўҪвҫцПВБРОКМвЈә
ЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј»
Ј»
ЈЁ2Ј©ЙИРОНіјЖНјЦР»ъЖчИЛПоДҝЛщ¶ФУҰЙИРОөДФІРДҪЗ¶ИКэОӘ ![]() Ј»
Ј»
ЈЁ3Ј©ҙУСЎәҪДЈПоДҝөД![]() ГыС§ЙъЦРЛж»ъСЎИЎ
ГыС§ЙъЦРЛж»ъСЎИЎ![]() ГыС§ЙъІОјУѧУәҪДЈРЛИӨРЎЧйСөБ·Ј¬ЗлУГБРҫЩ·ЁЈЁ»ӯКчЧҙНј»тБРұнЈ©ЗуЛщСЎИЎөД
ГыС§ЙъІОјУѧУәҪДЈРЛИӨРЎЧйСөБ·Ј¬ЗлУГБРҫЩ·ЁЈЁ»ӯКчЧҙНј»тБРұнЈ©ЗуЛщСЎИЎөД![]() ГыС§ЙъЦРЗЎәГУР
ГыС§ЙъЦРЗЎәГУР![]() ГыДРЙъЎў
ГыДРЙъЎў![]() ГыЕ®ЙъөДёЕВКЈ®
ГыЕ®ЙъөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,ЎчABCЦР, ЎПBAC=ЎПADB,BEЖҪ·ЦЎПABCҪ»ADУЪөгE,Ҫ»ACУЪөгF,№эөгEЧчEG//BCҪ»ACУЪөгG.
ЈЁ1Ј©ЗуЦӨ: AE=AF;
ЈЁ2Ј©ИфAG=4Ј¬AC=7Ј¬ЗуFGөДіӨ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҙУ2007Дк4ФВ18ИХҝӘКј,ОТ№ъМъВ·өЪБщҙОМбЛЩ,ДіҙОБРіөЖҪҫщМбЛЩv km/h.
ЈЁ1Ј©ИфМбЛЩЗ°БРіөөДЖҪҫщЛЩ¶ИОӘx km/h,РРК»1200kmөДВ·іМ,МбЛЩәуұИМбЛЩЗ°ЙЩУГ¶аіӨКұјдЈҝ
ЈЁ2Ј©Ифv=50,РРК»1200kmөДВ·іМ,МбЛЩәуЛщУГКұјдКЗМбЛЩЗ°өД ![]() Ј¬ЗуМбЛЩЗ°БРіөөДЖҪҫщЛЩ¶ИЈҝ
Ј¬ЗуМбЛЩЗ°БРіөөДЖҪҫщЛЩ¶ИЈҝ
ЈЁ3Ј©УГПаН¬өДКұјд,БРіөМбЛЩЗ°РРК»s km,МбЛЩәуұИМбЛЩЗ°¶аРРК»50km,ФтМбЛЩЗ°өДЖҪҫщЛЩ¶ИОӘkm/h.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРјЖЛгХэИ·өДКЗЈЁ Ј©
A.a2a3=a6
B.ЈЁ©Ғ2abЈ©2=4a2b2
C.ЈЁa2Ј©3=a5
D.a6ЎВa3=a2
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЕЧОпПЯ
ЦРЈ¬ЕЧОпПЯ![]() Ҫ»
Ҫ»![]() ЦбУЪ
ЦбУЪ![]() Ўў
Ўў![]() БҪөгЈЁөг
БҪөгЈЁөг![]() ФЪөг
ФЪөг![]() өДЧуІаЈ©Ј¬Ҫ«ёГЕЧОпПЯО»УЪ
өДЧуІаЈ©Ј¬Ҫ«ёГЕЧОпПЯО»УЪ![]() ЦбЙП·ҪЗъПЯјЗЧч
ЦбЙП·ҪЗъПЯјЗЧч![]() Ј¬Ҫ«ёГЕЧОпПЯО»УЪ
Ј¬Ҫ«ёГЕЧОпПЯО»УЪ![]() ЦбПВ·ҪІҝ·ЦСШ
ЦбПВ·ҪІҝ·ЦСШ![]() Цб·ӯХЫЈ¬·ӯХЫәуЛщөГЗъПЯјЗЧч
Цб·ӯХЫЈ¬·ӯХЫәуЛщөГЗъПЯјЗЧч![]() Ј¬ЗъПЯ
Ј¬ЗъПЯ![]() Ҫ»
Ҫ»![]() ЦбУЪөг
ЦбУЪөг![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ўў
Ўў![]() Ј®
Ј®
ЈЁ1Ј©ЗуЗъПЯ![]() ЛщФЪЕЧОпПЯПаУҰөДәҜКэұнҙпКҪЈ»
ЛщФЪЕЧОпПЯПаУҰөДәҜКэұнҙпКҪЈ»
ЈЁ2Ј©Зу![]() НвҪУФІөД°лҫ¶Ј»
НвҪУФІөД°лҫ¶Ј»
ЈЁ3Ј©өг![]() ОӘЗъПЯ
ОӘЗъПЯ![]() »тЗъПЯ
»тЗъПЯ![]() ЙПөДТ»ёц¶ҜөгЈ¬өг
ЙПөДТ»ёц¶ҜөгЈ¬өг![]() ОӘ
ОӘ![]() ЦбЙПөДТ»ёц¶ҜөгЈ¬ИфТФөг
ЦбЙПөДТ»ёц¶ҜөгЈ¬ИфТФөг![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() ОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈ¬Зуөг
ОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈ¬Зуөг![]() өДЧшұкЈ®
өДЧшұкЈ®

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com