
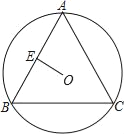
【题目】已知:⊙O为△ABC的外接圆,AB=AC,E是AB的中点,连OE,OE=![]() ,BC=8,则⊙O的半径为( )
,BC=8,则⊙O的半径为( )
A. 3 B. ![]() C.
C. ![]() D. 5
D. 5
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知线段![]() ,
,![]() ,线段
,线段![]() 在线段
在线段![]() 上运动,
上运动,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
![]()
(1)若![]() ,则
,则![]() ______
______![]() ;
;
(2)当线段![]() 在线段
在线段![]() 上运动时,试判断
上运动时,试判断![]() 的长度是否发生变化?如果不变请求出
的长度是否发生变化?如果不变请求出![]() 的长度,如果变化,请说明理由;
的长度,如果变化,请说明理由;
(3)我们发现角的很多规律和线段一样,如图②已知![]() 在
在![]() 内部转动,
内部转动,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,则
,则![]() 、
、![]() 和
和![]() 有何数量关系,请直接写出结果不需证明.
有何数量关系,请直接写出结果不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),
上一动点(不与B,C重合),
求证:![]() PA=PB+PC.
PA=PB+PC.

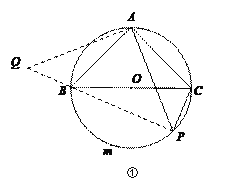
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
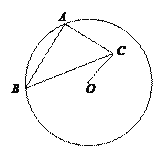
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.

(3)拓展延伸
如图,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 的
的![]() 边上的高,过点
边上的高,过点![]() 做
做![]() ,交直线
,交直线![]() 于点
于点![]() .
.
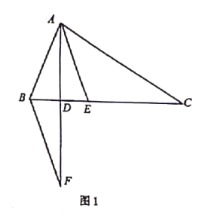
![]() 如图1,若
如图1,若![]() ,则
,则![]() ___ ____;
___ ____;
![]() 若
若![]() 中的
中的![]() ,则
,则![]() __ ____;(用
__ ____;(用![]() 表示)
表示)
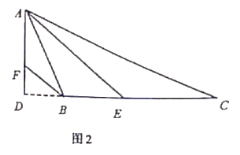
![]() 如图2,
如图2,![]() 中的结论还成立吗?若成立,说明理由;若不成立,请求出
中的结论还成立吗?若成立,说明理由;若不成立,请求出![]() .(用
.(用![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两条线段长分别是一元二次方程![]() 的两根,
的两根,
(1)解方程求两条线段的长。
(2)若把较长的线段剪成两段,使其与另一段围成等腰三角形,求等腰三角形的面积。
(3)若把较长的线段剪成两段,使其与另一段围成直角三角形,求直角三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在白纸上画两条长度均为![]() 且夹角为
且夹角为![]() 的线段
的线段![]() 、
、![]() ,然后你把一支长度也为
,然后你把一支长度也为![]() 的铅笔
的铅笔![]() 放在线段
放在线段![]() 上,将这支铅笔以线段
上,将这支铅笔以线段![]() 上的一点
上的一点![]() 为旋转中心旋转顺时针旋转一周。
为旋转中心旋转顺时针旋转一周。
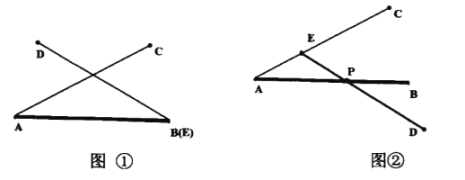
(1)若![]() 与
与![]() 重合,当旋转角为______时,这支铅笔与线段
重合,当旋转角为______时,这支铅笔与线段![]() 、
、![]() 围成的三角形是等腰三角形。
围成的三角形是等腰三角形。
(2)点![]() 从
从![]() 逐渐向
逐渐向![]() 移动,记
移动,记![]() :
:
①若![]() ,当旋转角为
,当旋转角为![]() 、______、______、______、
、______、______、______、![]() 、______时这支铅笔与线段
、______时这支铅笔与线段![]() 、
、![]() 共围成6个等腰三角形。
共围成6个等腰三角形。
②当这支铅笔与线段![]() 、
、![]() 正好围成5个等腰三角形时,求
正好围成5个等腰三角形时,求![]() 的取值范围。
的取值范围。
③当这支铅笔与线段![]() 、
、![]() 正好围成3个等腰三角形时,直接写出
正好围成3个等腰三角形时,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风“利奇马”给我县带来极端风雨天气,有一个水库8月9日8:00的水位为﹣0.1m(以10m为警戒线,记高于警戒线的水位为正)在以后的6个时刻测得的水位升降情况如下(记上升为正,单位:m)
时刻 | 1 | 2 | 3 | 4 | 5 | 6 |
升降 | 0.5 | ﹣0.4 | 0.6 | ﹣0.5 | 0.2 | ﹣0.8 |
(1)根据记录的数据,求第2个时刻该水库的实际水位;
(2)在这6个时刻中,该水库最高实际水位是多少?
(3)经过6次水位升降后,水库的水位超过警戒线了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
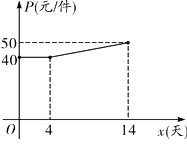
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com