
【题目】如图,菱形![]() 的边
的边![]() 轴,垂足为点
轴,垂足为点![]() ,顶点
,顶点![]() 在第二象限,顶点
在第二象限,顶点![]() 在
在![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() ,
,![]() )的图像同时经过顶点
)的图像同时经过顶点![]() 、
、![]() ,若点
,若点![]() 的横坐标为1,
的横坐标为1,![]() .则
.则![]() 的值为( )
的值为( )

A.![]() B.3C.
B.3C.![]() D.5
D.5
科目:初中数学 来源: 题型:
【题目】某公司为了更好治理污水质,改善环境,决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 200 | 160 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少1万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过78万元,你认为该公司有哪几种购买方案;
(3)在(2)间的条件下,若每月要求处理的污水量不低于1620吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表![]() 单位:环
单位:环![]() :
:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
甲 | 10 | 9 | 8 | 8 | 10 | 9 |
乙 | 10 | 10 | 8 | 10 | 7 | 9 |
根据表格中的数据,可计算出甲、乙两人的平均成绩都是9环.
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选______名队员参赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l3,l4与l1,l2分别相交于点A、B、C、D,且∠1+∠2=180°.
(1)直线l1与l2平行吗?为什么?
(2)点E在线段AD上,∠ABE=30°,∠BEC=62°,求∠DCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 与
与![]() 关于
关于![]() 轴对称,交
轴对称,交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 在
在![]() 外作直线
外作直线![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 于点
于点 ![]() .求证:
.求证:![]()
(3)如图2,如果![]() 沿
沿![]() 轴向右平移,
轴向右平移,![]() 边交
边交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 的延长线上的一点,且
的延长线上的一点,且![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,在
,在![]() 平移的过程中,
平移的过程中,![]() 的长度是否为定值,请说明理由.
的长度是否为定值,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
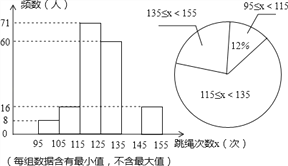
【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.

(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com