
 ��ͼ����֪���κ�����ͼ�����A��0��-3����B��
��ͼ����֪���κ�����ͼ�����A��0��-3����B�� ��
�� �����Գ���Ϊֱ��x=-
�����Գ���Ϊֱ��x=- ����P���������ϵ�һ���㣬����P�ֱ���PM��x���ڵ�M��PN��y���ڵ�N�����ı���PMON�Ϸֱ��ȡPC=
����P���������ϵ�һ���㣬����P�ֱ���PM��x���ڵ�M��PN��y���ڵ�N�����ı���PMON�Ϸֱ��ȡPC= MP��MD=
MP��MD= OM��OE=
OM��OE= ON��NF=
ON��NF= NP��
NP�� ��2+k��
��2+k�� ��
�� �����������ϣ�
�����������ϣ�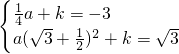 ��
��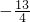 ��
�� ��2
��2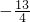 =x2+x-3��
=x2+x-3��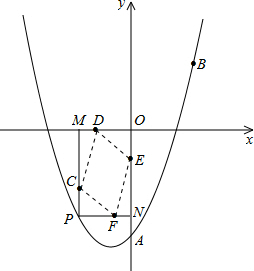
 MP��OE=
MP��OE= ON��
ON�� OM��NF=
OM��NF= NP��
NP��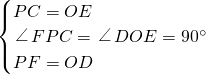
 m��MC=
m��MC= m��MD=
m��MD= n��PF=
n��PF= n��
n�� ����
����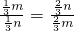 ������ã�m2=n2��
������ã�m2=n2�� ��
��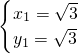 ��
��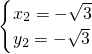 ��
�� ��
�� ����P2��-
����P2��- ��-
��- ����
���� ��
�� ��
�� ��
�� ��
�� ����P2��-
����P2��- ��-
��- ����P3��-3��3����P4��-1��1����
����P3��-3��3����P4��-1��1����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��һ�����㣬����P��x��Ĵ��ߣ�����ΪD��m��0��������ֱ��OA���ڵ�C��
��һ�����㣬����P��x��Ĵ��ߣ�����ΪD��m��0��������ֱ��OA���ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•���ͺ��أ���ͼ����֪���κ�����ͼ����A��6��0����B��-2��0���͵�C��0��-8����
��2013•���ͺ��أ���ͼ����֪���κ�����ͼ����A��6��0����B��-2��0���͵�C��0��-8����| 6 |
| 7 |
| 6 |
| 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
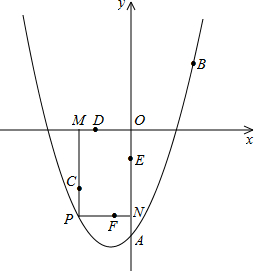 ��2013•���£���ͼ����֪���κ�����ͼ�����A��0��-3����B��
��2013•���£���ͼ����֪���κ�����ͼ�����A��0��-3����B��| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪���κ�����ͼ����x�ύ��A��2��0����B��6��0�����㣬��y�ύ�ڵ�D��0��4����
��ͼ����֪���κ�����ͼ����x�ύ��A��2��0����B��6��0�����㣬��y�ύ�ڵ�D��0��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪���κ�����ͼ��0��x��3.4�������ڸú����������Ա�����ȡֵ��Χ�ڣ�����˵����ȷ���ǣ�������
��ͼ����֪���κ�����ͼ��0��x��3.4�������ڸú����������Ա�����ȡֵ��Χ�ڣ�����˵����ȷ���ǣ��������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com