
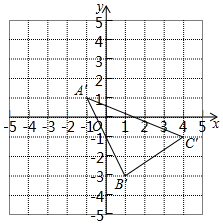
 在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).
在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).分析 (1)根据平面直角坐标系找出点A、B、C的位置,然后顺次连接即可,再利用△ABC所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解;
(2)根据网格结构找出点A、B平移后的对应点A′、B′的位置,然后顺次连接即可;
(3)根据向右平移横坐标加,向下平移纵坐标减求解即可.
解答 解:(1)如图所示: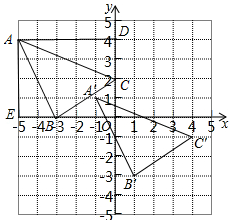
S△ABC=S矩形AEOD-S△ADC-S△BCO-S△AEB
=4×5-$\frac{1}{2}$×5×2-$\frac{1}{2}$×3×2-$\frac{1}{2}$×4×2
=20-5-3-4
=8;
(2)∵A(-5,4),A′(-1,1),
∴点A′由点A向右平移4个单位,然后向下平移3个单位得到.
∴△A′B′C′由△ABC向右平移4个单位,然后向下平移3个单位得到.
(3)由题意得,点P(m,n)对应点P′的坐标为(m+4,n-3).
故答案为:(m+4,n-3).
点评 本题考查了利用平移变换作图,三角形的面积计算,平移的性质,熟练掌握网格结构准确找出对应点的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
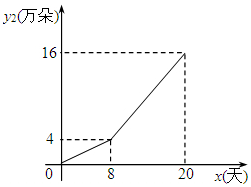 某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.
某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.| 时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
| 销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
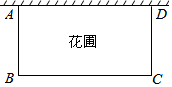 为了美化生活环境,小明的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
为了美化生活环境,小明的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
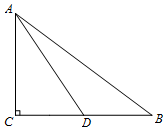 如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=$\frac{3}{4}$.
如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
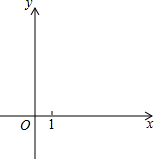 如图,抛物线y=ax2+bx-16a+4b交x轴负半轴于点A,交x轴正半轴于点B,交y轴正半轴于点C,且OA:OB=2:3.
如图,抛物线y=ax2+bx-16a+4b交x轴负半轴于点A,交x轴正半轴于点B,交y轴正半轴于点C,且OA:OB=2:3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com