Question

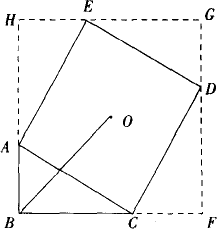
已知：如下图，△ABC中，∠ABC＝90°，AB＝3，BC＝5，以AC为一边向△ABC外作正方形AC－DE，求正方形的中心O与点B之间的线段长．

Answer 1

答案：
解析：

简解：分别延长BC到F，BA到H，使CF＝AB＝3，AH＝BC＝5，连结FD、HE并延长交于点G． 　　可证△ABC≌△CFD≌△EHA(SAS)和△CFD≌△DGE(ASA)， 　　∴△ABC≌△CFD≌△EHA≌△DGE． 　　∴四边形BFGH是边长为8的正方形， 　　又△CFD、△DGE、△EHA可以看成以点O为中心，将△ABC分别旋转90°、180°、270°而得到的， 　　∴点O也是正方形BFGH的中心． 　　∴OB＝＝4． 　　分析：从图形本身很难打开思路．若补成含有∠ABC且经过点D、E的正方形，OB便为这个正方形对角线长的一半，结论便是显然的． 　　简评：巧将图形补成正方形，使解题由阴霾变得明朗，正方形的特性得到充分利用．