
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
【答案】(1)120,90;(2)11种;(3)购买篮球40,足球60个时,y最小值为10200元.
【解析】
试题分析:(1)设一个篮球x元,则一个足球(x﹣30)元,根据“买两个篮球和三个足球一共需要510元”列出方程,即可解答;
(2)设购买篮球x个,足球(100﹣x)个,根据“篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元”,列出不等式组,求出x的取值范围,由x为正整数,即可解答;
,学校可用于购买这批篮球和足球的资金最多为10500元”,列出不等式组,求出x的取值范围,由x为正整数,即可解答;
(3)表示出总费用y,利用一次函数的性质,即可确定x的取值,即可确定最小值.
试题解析:(1)设一个篮球x元,则一个足球(x﹣30)元,由题意得:2x+3(x﹣30)=510,解得:x=120,∴一个篮球120元,一个足球90元;
(2)设购买篮球x个,足球(100﹣x)个,由题意可得: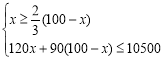 ,解得:40≤x≤50,∵x为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案;
,解得:40≤x≤50,∵x为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案;
(3)由题意可得y=120x+90(100﹣x)=30x+9000(40≤x≤50),∵k=30>0,∴y随x的增大而增大,∴当x=40时,y有最小值,y最小=30×40+9000=10200(元),所以当x=40时,y最小值为10200元.


科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A:∠B:∠C=l:2:3
B.三边长为a,b,c的值为1,2, ![]()
C.三边长为a,b,c的值为 ![]() ,2,4
,2,4
D.a2=(c+b)(c﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个说法中,正确的是( )
A. 相等的角是对顶角
B. 平移不改变图形的形状和大小,但改变直线的方向
C. 两条直线被第三条直线所截,内错角相等
D. 两直线相交形成的四个角相等,则这两条直线互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2(a>0)过A(﹣2,y1)、B(1,y2)两点,则下列关系式一定正确的是( )
A.y1>0>y2
B.y2>0>y1
C.y1>y2>0
D.y2>y1>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长 . ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com