
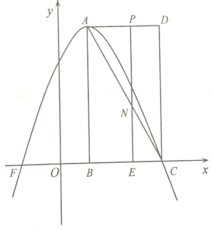
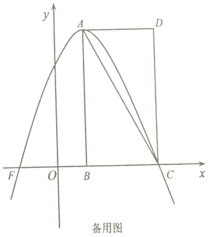
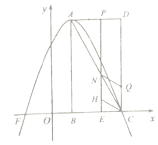
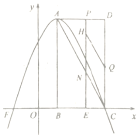
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 的坐标分别
的坐标分别![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 过点
过点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 匀速运动,过点
匀速运动,过点![]() 作
作![]() 轴,交对角线
轴,交对角线![]() 于点
于点![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
(1)求抛物线的解析式;
(2)若![]() 分
分![]() 的面积为
的面积为![]() 的两部分,求
的两部分,求![]() 的值;
的值;
(3)若动点![]() 从
从![]() 出发的同时,点
出发的同时,点![]() 从
从![]() 出发,以每秒1个单位的速度沿线段
出发,以每秒1个单位的速度沿线段![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() 为线段
为线段![]() 上一点.若以
上一点.若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,求
为顶点的四边形为菱形,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 的值为
的值为![]() 或
或![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)运用待定系数法求解;
(2)根据已知,证![]() ,
,![]() ,可得
,可得![]() 或
或![]() ;
;
(3)分两种情况:当![]() 为菱形的对角线时:由点
为菱形的对角线时:由点![]() ,
,![]() 的横坐标均为
的横坐标均为![]() ,可得
,可得![]() .求直线
.求直线![]() 的表达式为
的表达式为![]() ,再求N的纵坐标,得
,再求N的纵坐标,得![]() ,根据菱形性质得
,根据菱形性质得![]() ,可得
,可得![]() .在
.在![]() 中,得
中,得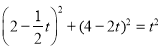 .同理,当
.同理,当![]() 为菱形的边时:由菱形
为菱形的边时:由菱形![]() 性质可得,
性质可得,![]() .由于
.由于![]() ,所以
,所以![]() .结合三角函数可得
.结合三角函数可得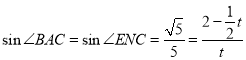 .
.
解:(1)因为,矩形![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 的坐标分别
的坐标分别![]() ,
,![]() ,
,![]() ,
,
所以A的坐标是(1,4),可设函数解析式为:![]()
把![]() 代入可得,a=-1
代入可得,a=-1
所以![]() ,即
,即![]() .
.
(2)因为PE∥CD
所以可得![]() .
.
由![]() 分
分![]() 的面积为
的面积为![]() 的两部分,可得
的两部分,可得![]()
所以![]() ,解得
,解得![]() .
.
所以,![]() 的值为
的值为![]()
![]() =
=![]() (秒).
(秒).
或![]() ,解得
,解得![]() .
.
所以,![]() 的值为
的值为![]()
![]() .
.
综上所述,![]() 的值为
的值为![]() 或
或![]() .
.
(3)当![]() 为菱形的对角线时:
为菱形的对角线时:
由点![]() ,
,![]() 的横坐标均为
的横坐标均为![]() ,可得
,可得
![]() .
.
设直线AC的解析式为![]() ,把A,C的坐标分别代入可得
,把A,C的坐标分别代入可得
![]()
解得
![]()
所以直线![]() 的表达式为
的表达式为![]() .
.
将点![]() 的横坐标
的横坐标![]() 代入上式,得
代入上式,得
![]() .
.
即![]() .
.
由菱形![]() 可得,
可得,![]() .
.
可得![]() .
.
在![]() 中,得
中,得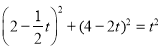 .
.
解得,![]() ,t2=4(舍).
,t2=4(舍).
当![]() 为菱形的边时:
为菱形的边时:
由菱形![]() 性质可得,
性质可得,![]() .
.
由于![]() ,
,
所以![]() .
.
因为![]() .
.
由![]() ,得
,得
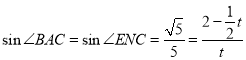 .
.
解得,![]() ,
,
综上所述,![]() 的值为
的值为![]() 或
或![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】“垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
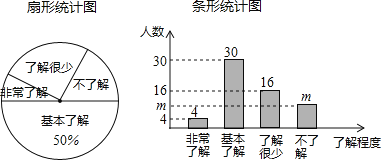
(1)接受问卷调查的学生共有 人,条形统计图中![]() 的值为 ;
的值为 ;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为 ;
(3)若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐,某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可售价100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降![]() 元,则每月可多销售5条.设每条裤子的售价为
元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于3800元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
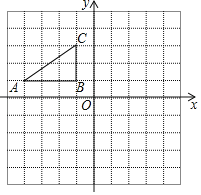
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3),请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出△ABC关于y轴对称图形△A2B2C2,则△A2B2C2与△A1B1C1的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
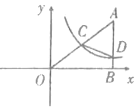
【题目】如图,在平面直角坐标系中,![]() 点的坐标为
点的坐标为![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象的一支经过
的图象的一支经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() .
.
(1)求该反比例函数的表达式;
(2)若函数![]() 与
与![]() 的图象的另一支交于点
的图象的另一支交于点![]() ,求三角形
,求三角形![]() 与四边形
与四边形![]() 的面积比.
的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的![]() ,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com