练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设，，…，(为大于0的自然数)．

    (1)探究是否为8的倍数，并用文字语言表述你所获得的结论；

    (2)若一个数的算术平方根是一个自然数，则称这个数是“完全平方数”．试找出，…，，…这一列数中从小到大排列的前4个完全平方数，并指出当满足什么条件时，为完全平方数(不必说明理由)

    解：(1)∵

    又为大于0的自然数，∴是8的倍数．

    这个结论用文字语言表述为：两个连续奇数的平方差是8的倍数．

    (2)这一列数中从小到大排列的前4个完全平方数为16，64，144，256．

    为一个完全平方数的2倍时，为完全平方数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

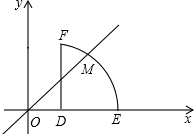    如图，扇形DEF的圆心角∠FDE=90°点D（d，0）在点E的左侧，d为大于0的实数，直线精英家教网y=
    		3
    x与
    EF
    交于点M，OM=2（O是坐标原点），以直线DF为对称轴的抛物线y=x2+px+q与x轴交于点E，
    （1）求点E的坐标；
    （2）抛物线y=x2+px+q与x轴的交点有可能都在原点的右侧吗？请说明理由；
    （3）设抛物线y=x2+px+q的顶点到x轴的距离为h，求h的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设a1=32-12，a2=52-32，…，an=（2n+1）2-（2n-1）2（n为大于0的自然数）．
    （1）探究an是否为8的倍数，并用文字表述出你所获得的结论；
    （2）若一个数的算术平方根是一个自然数，则称这个数是“完全平方数”，例如：1，4，9，16，…，是“完全平方数”．试写出a1，a2，a3，…，an，这一列数中从小到大排列的前4个“完全平方数”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某企业员工300人，生产A种产品，平均每人每年可创造利润m万元（m为大于零的常数），为减员增效，决定从中调配x人去生产新开发的B种产品，根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54m万元．
    （1）调配后，企业生产A种产品的年利润为
     
    万元，企业生产B种产品年利润为
     
    万元（用含x和m的代数式表示）．若设调配后企业全年总利润为y万元，则y与x的关系式y=
     
    ．
    （2）若要求调配后，企业生产A种产品的年利润不小于调配前企业利润的
    45
    ，生产B种产品的年利润大于调配前企业年利润的一半，应有哪几种调配方案？请设计出来．
    （3）比较（2）中的几种调配方案并指出其中哪种方案全年总利润最大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

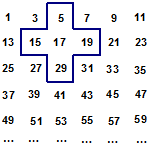    精英家教网将连续的奇数1，3，5，7，…，排成如图所示的数表，用十字框任意框出5个数．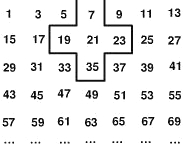
    探究规律一：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为
     
    ．
    结论：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是
     
    ．
    探究规律二：
    落在十字框中间且又是第二列的奇数是15，27，39…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列，第五列的奇数分别可表示为
     
    ．
    运用规律：
    （1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是
     
    ．这个奇数落在从左往右第
     
    列．
    （2）请你写出一个不能够框在十字框中间的且大于500的奇数：
     
    ．
    （3）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．精英家教网
    变通运用：
    若把这些奇数重新排列如右图，解答下列问题：
    （1）下列能被十字框框在中间的奇数是（
     
    　）
    A.841   B.1121   C.1263  D.1091
    （2）被框在十字框中的五个数之和可能是1925吗？说说你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某企业有员工300人，生产A种产品，平均每人每年可创造利润1万元（m为大于零的常数）．为减员增效，决定从中调配x人去生产新开发的B种产品．根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54万元．
    （1）调配后，企业生产A种产品的年利润为
    1.2（300-x）
    1.2（300-x）
     万元，企业生产B种产品的年利润为
    1.54x
    1.54x
     万元（用含x的代数式表示）．若设调配后企业全年总利润为y万元，则y关于x的函数解析式为
    y=0.34x+360
    y=0.34x+360
    ．（括号里填最简结果）
    （2）若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的
    4
    5
    ，生产B种产品的年利润大于调配前企业年利润的
    1
    2
    ，应有哪几种调配方案？请设计出来，并指出其中哪种方案全年总利润最大？

    查看答案和解析>>

    同步练习册答案