

 Οκ ±Θ§SΉν¥σ÷ΒΈΣ
Οκ ±Θ§SΉν¥σ÷ΒΈΣ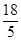 cm2;
cm2;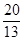
 sΜρ
sΜρ sΜρ
sΜρ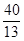 s ±Θ§ΓςAPQ «Β»―ϋ»ΐΫ«–ΈΘ°
s ±Θ§ΓςAPQ «Β»―ϋ»ΐΫ«–ΈΘ°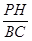 =
=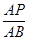 Θ§¥”Εχ«σ≥ωABΘ§‘ΌΗυΨί
Θ§¥”Εχ«σ≥ωABΘ§‘ΌΗυΨί =
=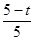 Θ§ΒΟ≥ωPH=3©¹
Θ§ΒΟ≥ωPH=3©¹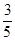 tΘ§‘ρΓςAQPΒΡΟφΜΐΈΣΘΚ
tΘ§‘ρΓςAQPΒΡΟφΜΐΈΣΘΚ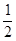 AQ•PH=
AQ•PH=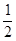 tΘ®3©¹
tΘ®3©¹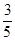 tΘ©Θ§ΉνΚσΫχ––’ϊάμΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
tΘ©Θ§ΉνΚσΫχ––’ϊάμΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ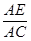 =
=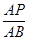 Θ§«σ≥ωAE=©¹
Θ§«σ≥ωAE=©¹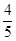 t+4Θ§‘ΌΗυΨίQE=AE©¹AQΘ§QE=
t+4Θ§‘ΌΗυΨίQE=AE©¹AQΘ§QE=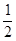 QCΒΟ≥ω©¹
QCΒΟ≥ω©¹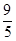 t+4=©¹
t+4=©¹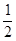 t+2Θ§‘Ό«σtΦ¥Ω…ΘΜ
t+2Θ§‘Ό«σtΦ¥Ω…ΘΜ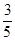 t+3Θ§”κΘ®2Θ©Ά§άμΒΟΘΚQD=©¹
t+3Θ§”κΘ®2Θ©Ά§άμΒΟΘΚQD=©¹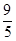 t+4Θ§¥”Εχ«σ≥ωPQ=
t+4Θ§¥”Εχ«σ≥ωPQ=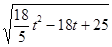 Θ§
Θ§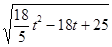 =tΘ§ΔέΒ±PQ=APΘ§Φ¥
=tΘ§ΔέΒ±PQ=APΘ§Φ¥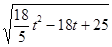 =5©¹tΘ§‘ΌΖ÷±πΦΤΥψΦ¥Ω…
=5©¹tΘ§‘ΌΖ÷±πΦΤΥψΦ¥Ω…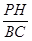 =
=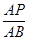 Θ§
Θ§ =
=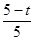 Θ§
ȧ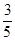 tȧ
tΘ§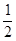 ΓΝAQΓΝPH=
ΓΝAQΓΝPH=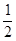 ΓΝtΓΝΘ®3©¹
ΓΝtΓΝΘ®3©¹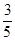 tΘ©=©¹
tΘ©=©¹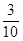 Θ®t©¹
Θ®t©¹ Θ©2+
Θ©2+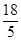 Θ§
Θ§ Οκ ±Θ§SΉν¥σ÷ΒΈΣ
Οκ ±Θ§SΉν¥σ÷ΒΈΣ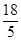 cm2Θ°
cm2Θ°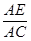 =
=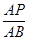 Θ§
Θ§ =
=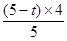 =©¹
=©¹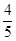 t+4
t+4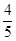 t+4©¹t=©¹
t+4©¹t=©¹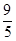 t+4Θ§
t+4Θ§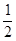 QC=
QC=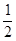 Θ®4©¹tΘ©=©¹
Θ®4©¹tΘ©=©¹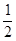 t+2Θ§
t+2Θ§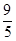 t+4=©¹
t+4=©¹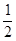 t+2Θ§
t+2Θ§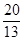 Θ§
Θ§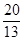 ΘΦ4Θ§
ΘΦ4Θ§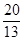 sΘΜ
sΘΜ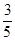 t+3Θ§”κΘ®2Θ©Ά§άμΒΟΘΚQD=AD©¹AQ=©¹
t+3Θ§”κΘ®2Θ©Ά§άμΒΟΘΚQD=AD©¹AQ=©¹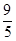 t+4
t+4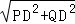 =
=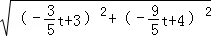 =
=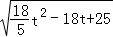 Θ§
Θ§ ΘΜ
ΘΜ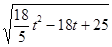 =t ±Θ§ΫβΒΟΘΚt2=
=t ±Θ§ΫβΒΟΘΚt2= Θ§t3=5ΘΜ
Θ§t3=5ΘΜ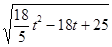 =5©¹t ±Θ§ΫβΒΟΘΚt4=0Θ§t5=
=5©¹t ±Θ§ΫβΒΟΘΚt4=0Θ§t5=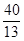 ΘΜ
ΘΜ sΜρ
sΜρ sΜρ
sΜρ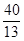 s ±Θ§ΓςAPQ «Β»―ϋ»ΐΫ«–ΈΘ°
s ±Θ§ΓςAPQ «Β»―ϋ»ΐΫ«–ΈΘ°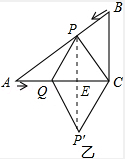
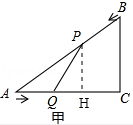



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΒΞ―ΓΧβ
»γΆΦΘ§œ¬Ν––ΈΉ¥ΒΡ±ΏΩρΘ§≤ΜœύΥΤΒΡ «Θ®ΓΓΓΓΘ©
|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΒΞ―ΓΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ≤Μœξ Χβ–ΆΘΚΧνΩ’Χβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com