
【题目】根据问题进行计算:
(1)计算: ![]() ×
× ![]() ﹣4×
﹣4× ![]() ×(1﹣
×(1﹣ ![]() )0;
)0;
(2)已知三角形两边长为3,5,要使这个三角形是直角三角形,求出第三边的长.
【答案】
(1)解:原式=2 ![]() ×
× ![]() ﹣4×
﹣4× ![]() ×1=2
×1=2 ![]() ﹣
﹣ ![]() =
= ![]() ;
;
(2)解:设第三边长为x,下面分两种情况讨论:
(i)当x为斜边时,由勾股定理,得x= ![]() ;
;
(ii)当x为直角边时,由勾股定理得x=4,
则第三边的长为 ![]() 或4.
或4.
【解析】(1)原式利用二次根式的乘法法则,以及零指数幂法则计算即可得到结果;(2)设第三边长为x,分x为斜边与5是斜边两种情况,利用勾股定理求出即可.
【考点精析】关于本题考查的零指数幂法则和二次根式的混合运算,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);二次根式的混合运算与实数中的运算顺序一样,先乘方,再乘除,最后加减,有括号的先算括号里的(或先去括号)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论: ①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .
.
其中正确的序号是(把你认为正确的都填上).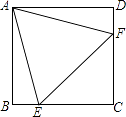
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC. 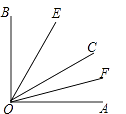
(1)若∠AOB=90°,∠AOC=40°,求∠EOF的度数;
(2)若∠AOB=a,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q. 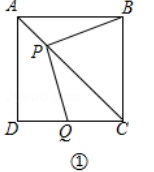
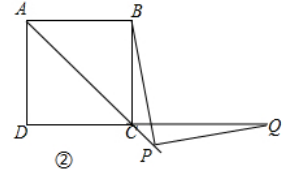
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的两边
的两边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() >0)与
>0)与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,若
,若![]() ,且
,且![]() 的面积是5,则
的面积是5,则![]() 的值为_______.
的值为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com