练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    利用“三角形内角和”性质，可以得到三角形的外角性质？如下图，
    ∵∠ACD是△ABC的外角，
    ∴∠ACD与∠ACB互为（    ），
    即∠ACD＝180°－∠ACB。
    ①又∵∠A＋∠B＋∠ACB＝（    ），
    ∴∠A＋∠B＝（    ）。
    ②由①、②，得∠ACD＝（    ）＋（    ）。
    ∴∠ACD＞∠A，∠ACD＞∠B
    由上述（2）的说理，可以得到三角形外角的性质如下：三角形的一个外角等于（    ）；三角形的一个外角大于（    ）。
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

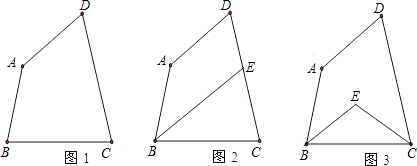
    精英家教网利用三角形内角和，探究四边形内角和：
    如图，∠A、∠B、∠C、∠D是四边形的四个内角，连接AC，因为
     
    ，所以
     
    ，即四边形内角和为
     
    ．
    利用上述结论解题：四边形ABCD中，∠A=140°，∠D=80°．
    （1）如图1，若∠B=∠C，试求出∠C的度数；
    （2）如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；
    （3）如图3，若∠ABC和∠BCD的角平分线交于点E，试求出∠BEC的度数．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2012年北师大版初中数学八年级下6.5三角形内角和定理的证明练习卷（解析版） 题型：解答题

    请你利用“三角形内角和定理”证明“四边形的内角和等于360°”.四边形ABCD如图所示.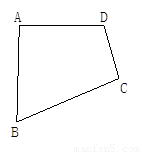

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    利用三角形内角和，探究四边形内角和：
    如图，∠A、∠B、∠C、∠D是四边形的四个内角，连接AC，因为______，所以______，即四边形内角和为______．
    利用上述结论解题：四边形ABCD中，∠A=140°，∠D=80°．
    （1）如图1，若∠B=∠C，试求出∠C的度数；
    （2）如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；
    （3）如图3，若∠ABC和∠BCD的角平分线交于点E，试求出∠BEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图, △中, 是边上的高线, 是一条角平分线,它们相交于点,

    已知,求的度数。

    【解析】此题利用三角形内角和，外角，角平分线解答

     

    查看答案和解析>>

    科目：初中数学 来源：2014届浙江省七年级下学期期中考试数学卷（解析版） 题型：解答题

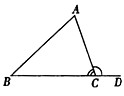
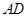    如图, △中, 是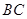边上的高线, 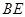是一条角平分线,它们相交于点,

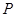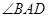    已知,求的度数。

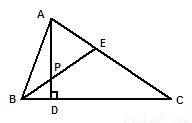
    【解析】此题利用三角形内角和，外角，角平分线解答

     

    查看答案和解析>>

    同步练习册答案