
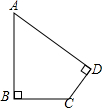
 有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为234m2.
有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为234m2. 分析 连接AC,则△ABC和△ACD均为直角三角形,根据AB,BC可以求出AC,根据AC,CD可以求出AD,根据直角三角形面积计算可以求出△ABC和△ACD的面积,四边形ABCD的面积为两个直角三角形面积之和.
解答 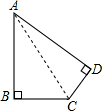 解:连接AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和,
解:连接AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和,
在Rt△ABC中,AC为斜边,
则AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25(m),
在Rt△ACD中,AC为斜边
则AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{2{5}^{2}-{7}^{2}}$═24(m),
四边形ABCD面积S=$\frac{1}{2}$AB×BC+$\frac{1}{2}$AD×CD=$\frac{1}{2}$×20×25+$\frac{1}{2}$×7×24=234(m2).
答:此块地的面积为234平方米.
故答案为:234m2.
点评 本题考查了勾股定理在实际生活中的应用以及直角三角形面积计算,本题中正确的运用勾股定理计算AC是解题的关键.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源:2016-2017学年河南省七年级下学期第一次月考(3月)数学试卷(解析版) 题型:填空题
如图, ∥
∥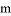 ,∠1=120°,∠A=55°,则∠ACB的大小是______.
,∠1=120°,∠A=55°,则∠ACB的大小是______.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com